Đếm phân số là một trong những kỹ năng toán học hữu ích nhất để phát triển. Trước khi thực hiện các phép tính về phân số, hãy học cách nhận biết các bộ phận và các dạng của phân số. Sau đó, bạn có thể cộng hoặc trừ chúng. Đối với các phép tính phức tạp hơn, hãy học cách nhân và chia phân số. Thông thường, bạn cũng sẽ cần đơn giản hóa hoặc giảm các phân số.
Bươc chân
Phương pháp 1/4: Nhận biết phân số
Bước 1. Tìm phân số
Các phân số được viết dưới dạng một số ở trên vạch chia và một số khác ở dưới vạch.
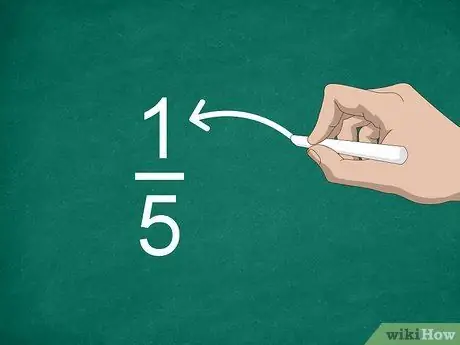
Bước 2. Xác định tử số
Số ở trên dòng được gọi là tử số và cho biết phân số có bao nhiêu phần.
Ví dụ, trong phân số 1/5, “1” là tử số
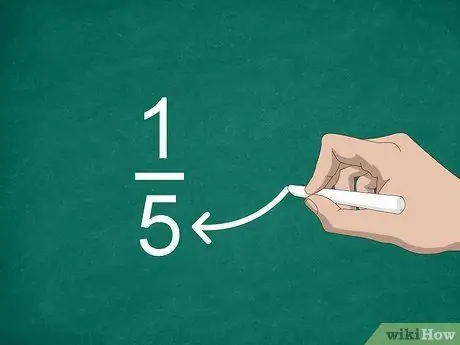
Bước 3. Tìm mẫu số
Số đặt dưới dòng được gọi là mẫu số. Giá trị này cho biết số phần "cấu tạo" một số nguyên.
Ví dụ, trong phân số 1/5, "5" là mẫu số nên phân số có năm phần
Bước 4. Xác định xem các phân số là phân số hợp lý hay phân số không đúng
Nếu tử số nhỏ hơn mẫu số thì phân số là phân số tự nhiên. Trong phân số không đúng, tử số lớn hơn mẫu số.
- Ví dụ, 3/4 là một phân số hợp lý và 5/3 là một phân số không đúng.
- Nếu bạn có một số nguyên bao gồm một phân số, số đó được gọi là hỗn số. Ví dụ: 1 1/2 là hỗn số.
Phương pháp 2/4: Cộng hoặc Trừ phân số
Bước 1. Nhận biết các phân số cùng mẫu số
Nếu bạn cần cộng hoặc trừ phân số, mỗi phân số phải có cùng mẫu số trước khi bạn thực hiện phép tính. Quan sát mẫu số của mỗi phân số để đảm bảo rằng chúng đều bằng nhau (tương tự).
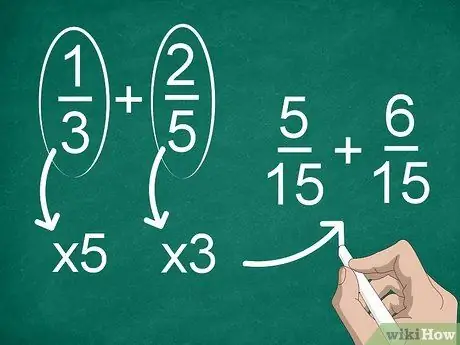
Bước 2. Tìm mẫu số chung nếu mỗi phân số có mẫu số khác nhau
Nếu các mẫu số không giống nhau, bạn sẽ cần phải thay đổi các phân số để có cùng mẫu số. Để tìm một mẫu số chung, hãy nhân mỗi phân số với mẫu số của phân số kia.
Ví dụ, để tìm một mẫu số chung trong 1/3 + 2/5, hãy nhân “1” và “3” với “5”, sau đó nhân “2” và “5” với “3”. Bây giờ, bạn có thêm 5/15 + 6/15. Sau đó, bạn có thể tính toán các phân số
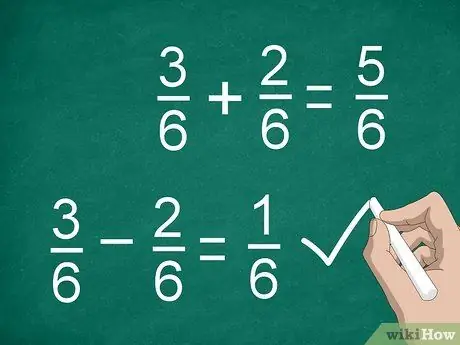
Bước 3. Cộng hoặc trừ các tử số để tính phân số
Khi bạn đã tìm được mẫu số chung và nhân các tử số (nếu cần), bạn đã sẵn sàng cộng hoặc trừ. Cộng hoặc trừ các tử số và đặt kết quả phía trên đường phân chia. Viết mẫu số chung dưới dòng.
- Ví dụ, 3/6 - 2/6 = 1/6.
- Không cộng hoặc trừ các mẫu số.
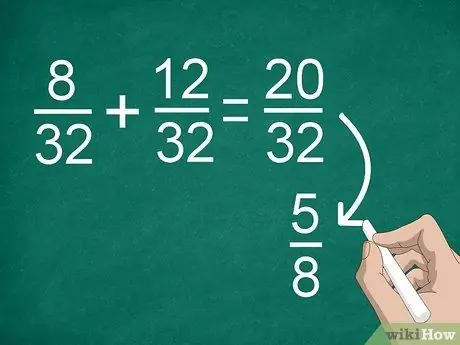
Bước 4. Đơn giản hóa kết quả nếu cần
Nếu trước đây bạn cần tìm một mẫu số chung, bạn có thể nhận được một phân số lớn mà bạn có thể đơn giản hóa. Ví dụ: nếu bạn thêm 8/32 +12/32, bạn sẽ nhận được kết quả là “20/32”. Phân số này có thể được đơn giản hóa thành "5/8".
Phương pháp 3/4: Nhân và đơn giản hóa phân số
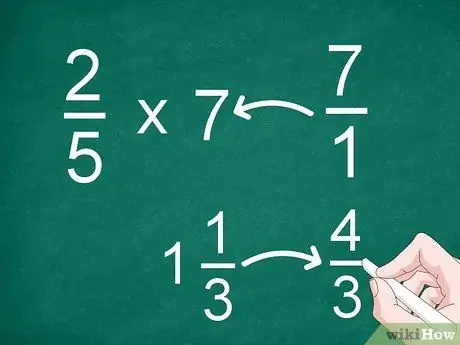
Bước 1. Chuyển hỗn số hoặc số nguyên thành phân số không đúng
Để thực hiện phép nhân dễ dàng hơn, bạn cần chuyển mỗi số thành một phân số hợp lý hoặc không đúng. Nếu bạn có số nguyên hoặc hỗn số cần nhân, trước tiên hãy chuyển chúng thành một phân số chung (tự nhiên hoặc không đúng).
- Ví dụ: để nhân 2/5 với 7, hãy chuyển "7" thành một phân số. Sau đó, bạn có thể nhân 2/5 với 7/1.
- Nếu bạn có hỗn số như 1 1/3, hãy chuyển nó thành phân số không đúng (“4/3”) trước khi nhân.
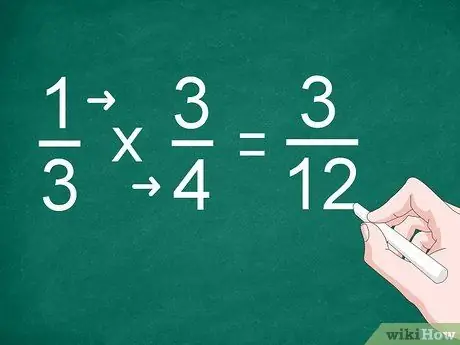
Bước 2. Nhân từng tử số và mẫu số
Thay vì thực hiện phép cộng, hãy nhân tử số và viết kết quả lên trên vạch chia. Bạn cũng cần nhân các mẫu số và viết kết quả dưới dòng.
Ví dụ, để nhân 1/3 với 3/4, hãy nhân “1” với “3” để lấy tử số. Nhân “3” với “4” để được mẫu số. Câu trả lời cho phép nhân là "3/12"
Bước 3. Đơn giản hóa kết quả
Thông thường, bạn sẽ cần phải giảm kết quả về một dạng đơn giản hơn, đặc biệt nếu ban đầu bạn có các phân số không tự nhiên. Tìm thừa số chung lớn nhất và sử dụng nhân tử đó để đơn giản hóa tử số và mẫu số.
Ví dụ: đối với phân số 3/12, nhân tử chung lớn nhất giữa “3” và “12” là “3”. Chia từng phần tử của phân số cho “3” cho đến khi bạn nhận được phân số “1/4”
Phương pháp 4/4: Chia phân số
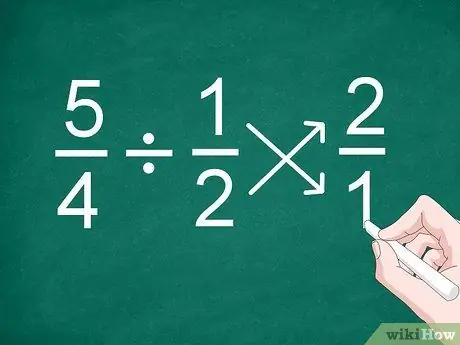
Bước 1. Đảo vị trí của phân số thứ hai
Cách đơn giản nhất để chia các phân số, ngay cả các phân số có mẫu số khác nhau, là đảo ngược vị trí của phân số thứ hai trước khi bạn tính kết quả.
Ví dụ, đối với bài toán 5/4 1/2, hãy đảo ngược vị trí của phân số “1/2” để trở thành “2/1”
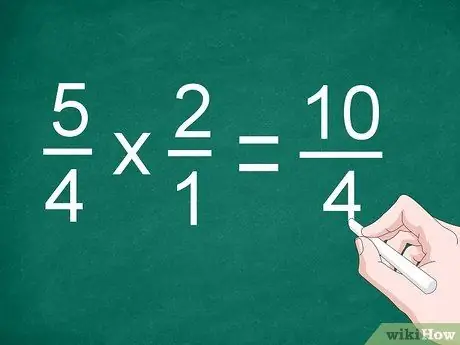
Bước 2. Nhân tử số và mẫu số
Nhân phân số trực tiếp với nhân tử số. Viết kết quả lên trên vạch chia, sau đó nhân với mẫu số. Ghi tích của các mẫu số dưới dòng.
Đối với ví dụ trước, nhân 5/4 với 2/1 để được "10/4"
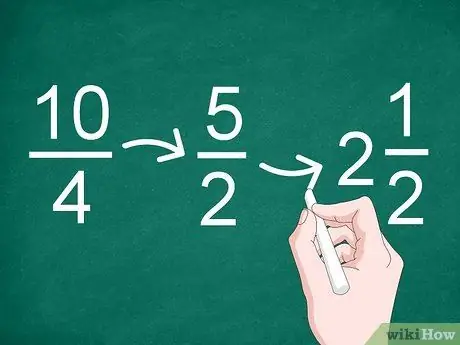
Bước 3. Đơn giản hóa kết quả nếu cần thiết
Nếu kết quả của phép chia là một phân số không đúng hoặc có thể bị rút gọn, hãy đơn giản hóa phân số. Sử dụng nhân tử chung lớn nhất để rút gọn phân số.
- Ví dụ: thừa số chung lớn nhất trong phân số 10/4 là “2” vì vậy kết quả của việc đơn giản hóa trở thành “5/2” (10 chia cho 2 và 4 chia cho 2).
- Vì kết quả của việc đơn giản hóa là một phân số không đúng, bạn có thể chuyển nó thành một số nguyên và một phân số (hỗn số). Do đó, 5/2 có thể được đổi thành “2”.
Lời khuyên
- Nếu bạn đang làm việc với các phân số phức tạp, bạn sẽ cần thực hiện một số bước bổ sung để đơn giản hóa phân số. Tuy nhiên, bản thân sự đơn giản hóa này là một phần bắt buộc của quá trình tính toán.
- Luôn viết các phân số ngay ngắn để giảm nguy cơ tính toán sai.
