Đối với hầu hết mọi người, phân số là phép tính phức tạp đầu tiên phải trải qua. Khái niệm về phân số khá khó và đòi hỏi bạn phải học những điều kiện đặc biệt mới có thể làm được. Bởi vì phân số có các quy tắc đặc biệt để cộng, trừ, nhân và chia, nhiều người nhầm lẫn về nó. Tuy nhiên, với nhiều thực hành, bất cứ ai cũng có thể học và hoàn thành các phép tính liên quan đến phân số.
Bươc chân
Phương pháp 1/5: Hiểu về phân số
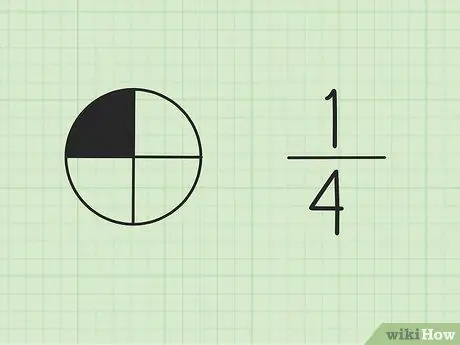
Bước 1. Hiểu rằng phân số là một phần của tổng thể
Số ở trên cùng được gọi là tử số và đại diện cho số phần của tổng số. Con số ở dưới cùng được gọi là mẫu số, đại diện cho tổng số phần.
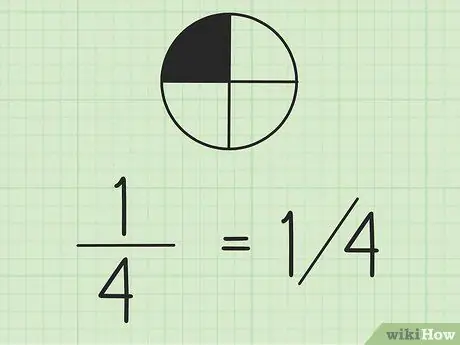
Bước 2. Hãy nhớ rằng bạn có thể viết phân số bằng dấu gạch chéo
Số bên trái là tử số và số bên phải là mẫu số. Nếu bạn đang làm việc với các phân số trên cùng một dòng, bạn nên viết tử số ở trên mẫu số.
Ví dụ, nếu bạn lấy một trong bốn lát bánh pizza, bạn có bánh pizza. Nếu bạn có 7/3 chiếc bánh pizza, điều đó có nghĩa là bạn có hai chiếc bánh pizza nguyên miếng cộng với 1 trong 3 miếng bánh pizza
Phương pháp 2/5: Sự khác biệt giữa hỗn số và phân số đơn giản
Bước 1. Hiểu rằng hỗn số bao gồm số nguyên và phân số, ví dụ 2 1/3 hoặc 45 1/2
Thông thường, bạn phải chuyển hỗn số sang dạng đơn giản hơn để cộng, trừ, nhân hoặc chia.
Bước 2. Đổi hỗn số bằng cách nhân số nguyên với mẫu số ở phân số, rồi cộng với tử số
Viết kết quả dưới dạng tử số, trong khi mẫu số không thay đổi.
Ví dụ, để chuyển 2 1/3 thành một phân số đơn giản, hãy nhân 2 với 3, sau đó cộng 1 và được 7/3
Bước 3. Chuyển phân số đơn giản thành hỗn số bằng cách chia tử số cho mẫu số
Toàn bộ kết quả của phép chia được viết dưới dạng số nguyên và phần còn lại của phép chia được viết dưới dạng tử số của phân số. Mẫu số không thay đổi.
Ví dụ, để chuyển 7/3 thành hỗn số, hãy chia 7 cho 3 để được 2 với dư là 1. Vậy hỗn số là 2 1/3. Chỉ có thể chuyển các phân số đơn giản thành hỗn số nếu tử số lớn hơn mẫu số
Phương pháp 3/5: Cộng và Trừ phân số
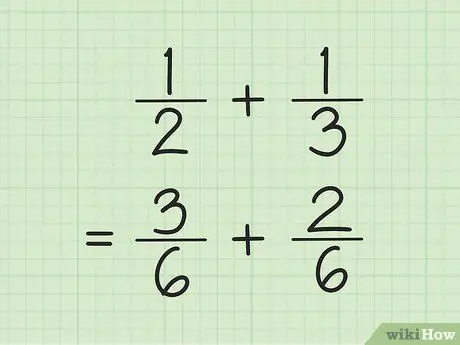
Bước 1. Tìm mẫu số chung để cộng trừ phân số
Mẹo, nhân các số ở mẫu số, sau đó nhân mỗi tử số với số được sử dụng để tìm mẫu số. Đôi khi, bạn có thể tìm LCM (bội số chung nhỏ nhất) cho mẫu số bằng cách nhân các mẫu số với nhau.
Ví dụ, để cộng và 1/3, trước tiên hãy tìm LCM (bội chung nhỏ nhất) của hai mẫu số bằng cách nhân với nhau. Do đó, bạn nhân 2 với 3 để được LCM 6. Nhân 1 với 3 để được 3 là tử số mới của phân số đầu tiên. Nhân 1 với 2 để được 2 là tử số mới của phân số thứ hai. Các phân số mới của bạn là 3/6 và 2/6
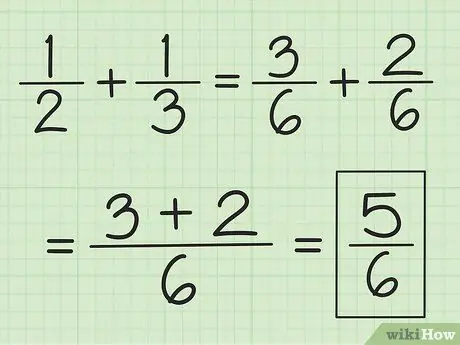
Bước 2. Cộng hai tử số với nhau và không thay đổi mẫu số
Ví dụ: 3/6 cộng với 2/6 là 5/6 và 2/6 cộng với 1/6 là 3/6
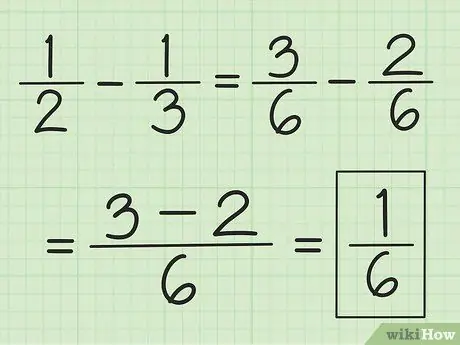
Bước 3. Sử dụng một kỹ thuật tương tự cho phép trừ
Tìm LCM của các mẫu số trước, nhưng thay vì cộng chúng, hãy lấy số của tử số thứ nhất trừ đi số thứ hai.
Ví dụ, để trừ 1/3 với 1/2, trước tiên hãy đổi các phân số thành 3/6 và 2/6, sau đó trừ 3 đi 2 để được 1. Kết quả là 1/6
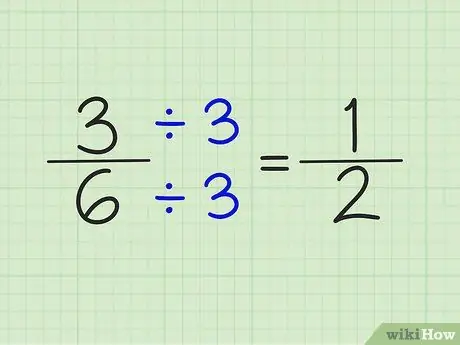
Bước 4. Đơn giản hóa phân số bằng cách chia tử số và mẫu số cho cùng một số
Ví dụ, số 5/6 không thể được đơn giản hóa. Tuy nhiên, 3/6 có thể được đơn giản hóa bằng cách chia tử số và mẫu số cho số 3. Kết quả là phân số 1/2
Bước 5. Chuyển phân số thành hỗn số nếu tử số lớn hơn mẫu số
Phương pháp 4/5: Nhân và Chia phân số
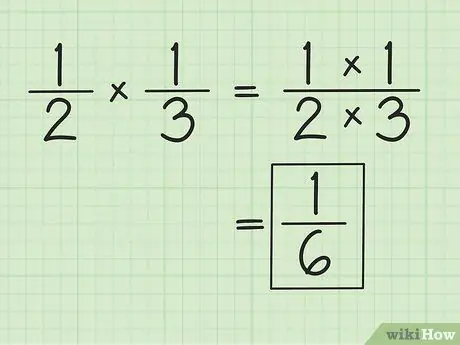
Bước 1. Nhân riêng tử số và mẫu số để nhân phân số
Ví dụ, khi nhân với 1/3, kết quả là 1/6 (1 nhân 1 và 2 nhân 3). Bạn không cần phải khớp các mẫu số khi nhân phân số. Đơn giản hóa hoặc sửa đổi kết quả thu được, nếu cần
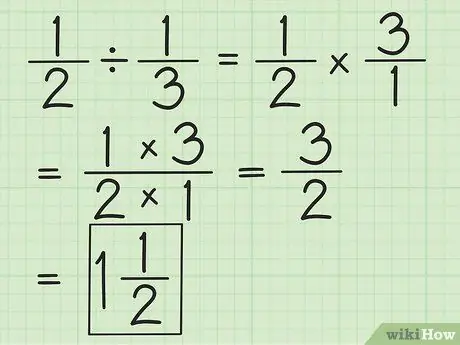
Bước 2. Chia hai phân số bằng cách đảo phân số thứ hai, sau đó nhân cả hai
Ví dụ, nếu bạn muốn chia 1/2 cho 1/3, trước tiên hãy đảo ngược phân số thứ hai thành 3/1. Nhân với 3/1 và được 3/2. Đơn giản hóa phân số hoặc chuyển đổi thành hỗn số, nếu có thể
Phương pháp 5/5: Làm việc với các phân số phức tạp
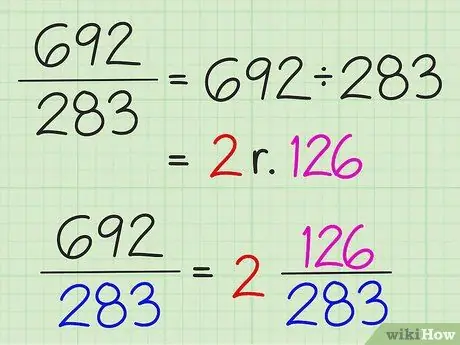
Bước 1. Làm tất cả các phân số theo cùng một cách, ngay cả khi vấn đề có vẻ rất phức tạp
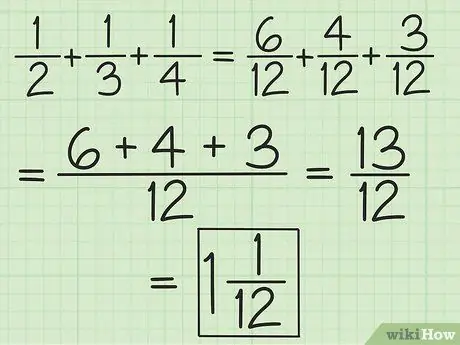
Bước 2. Ghép các mẫu số cho tất cả các phân số hoặc làm việc theo cặp bắt đầu từ trái sang phải để cộng và trừ nhiều hơn hai phân số
Ví dụ: để thêm 1/2, 1/3 và 1/4, bạn có thể thay đổi chúng thành 6/12, 4/12 và 3/12 để lấy 13/12 hoặc bạn có thể thêm 3/6 và 2 / 6 nên bạn nhận được 5/6, sau đó thêm 5/6 và 1/4 (lấy các mẫu số bằng nhau để phân số thứ hai trở thành 3/12) để được 13/12 (10/12 cộng với 3/12). Chuyển nó thành hỗn số, là 1 1/12
Lời khuyên
- Hãy nhớ rằng bạn đã học khá nhiều môn toán. Toán học giống như một ngôn ngữ mà bạn có thể phát âm trôi chảy, và bây giờ bạn đang cố gắng học đọc và viết nó.
- Hãy nhớ luôn đơn giản hóa kết quả cuối cùng của phép tính, cho dù bài toán của bạn ở dạng phân số thông thường, hỗn số hay phân số phức tạp.
