- Tác giả Jason Gerald gerald@how-what-advice.com.
- Public 2024-02-01 14:16.
- Sửa đổi lần cuối 2025-01-23 12:52.
Mọi người đều có thể học Toán cho dù họ đã ở giai đoạn cao hơn ở trường hay chỉ muốn trau dồi kiến thức cơ bản một lần nữa. Sau khi thảo luận về cách để trở thành một người học tốt môn Toán, bài viết này sẽ dạy bạn những tiến trình cơ bản về toán và sẽ cung cấp cho bạn những yếu tố cơ bản bạn sẽ cần học trong mỗi lần luyện tập. Sau đó, bài viết này sẽ thảo luận về những điều cơ bản của việc học số học, sẽ giúp ích cho cả trẻ em tiểu học và tất cả những ai muốn tìm hiểu những kiến thức cơ bản của lĩnh vực khoa học này.
Bươc chân
Phần 1/6: Các Bí Quyết Để Trở Thành Học Sinh Giỏi Toán

Bước 1. Xuất hiện trong lớp
Khi nghỉ học, bạn nên học các khái niệm từ các bạn cùng lớp hoặc từ sách giáo khoa của mình. Bạn sẽ không bao giờ nhận được bản tóm tắt văn bản từ một người bạn nhiều như bạn nhận được từ giáo viên của mình.
- Đến lớp đúng giờ. Thay vào đó, hãy đến sớm một chút và mở vở của bạn đúng chỗ, mở sách giáo khoa và lấy máy tính ra để bạn sẵn sàng bắt đầu khi giáo viên sẵn sàng dạy.
- Chỉ trốn học nếu bạn bị ốm. Nếu bạn thực sự nghỉ học, hãy hỏi các bạn cùng lớp để tìm hiểu xem giáo viên đang nói gì và bài tập về nhà đã được giao.

Bước 2. Làm việc với giáo viên của bạn
Nếu giáo viên của bạn đang giải quyết một vấn đề trước lớp, hãy làm việc với giáo viên bằng cách giải quyết vấn đề đó trong vở của bạn.
- Đảm bảo ghi chú của bạn rõ ràng và dễ đọc. Đừng chỉ viết câu hỏi. Cũng viết ra bất cứ điều gì giáo viên nói có thể cải thiện sự hiểu biết của bạn về các khái niệm đang được giải thích.
- Hoàn thành các câu hỏi mẫu do giáo viên của bạn đưa ra. Khi giáo viên đi xung quanh lớp khi bạn làm việc, hãy trả lời các câu hỏi được đặt ra.
- Tham gia khi giáo viên giải quyết một vấn đề. Đừng đợi giáo viên gọi cho bạn. Đề nghị trả lời khi bạn biết câu trả lời và giơ tay để đặt câu hỏi nếu bạn không chắc chắn về tài liệu đang được giảng dạy.

Bước 3. Làm bài tập về nhà cùng ngày với bài tập của bạn
Nếu bạn làm bài tập về nhà trong cùng một ngày, khái niệm đó vẫn còn mới trong tâm trí bạn. Đôi khi, hoàn thành bài tập về nhà của bạn trong cùng một ngày là không thể. Hãy chắc chắn rằng bài tập về nhà của bạn đã được hoàn thành trước khi bạn đến lớp.

Bước 4. Làm việc bên ngoài lớp học nếu bạn cần giúp đỡ
Đến thăm giáo viên của bạn trong giờ giải lao hoặc trong giờ hành chính.
- Nếu bạn có Trung tâm Toán học tại trường học của mình, hãy tìm hiểu giờ mở cửa của trung tâm đó và yêu cầu trợ giúp.
- Tham gia một nhóm học tập. Một nhóm học tốt thường bao gồm 4 hoặc 5 người với các mức độ năng lực khác nhau. Nếu bạn là học sinh "C" trong môn Toán, hãy tham gia một nhóm gồm 2 hoặc 3 học sinh có điểm "A" hoặc "B" để bạn có thể nâng cao kỹ năng của mình. Tránh tham gia một nhóm sinh viên có điểm thấp hơn của bạn.
Phần 2/6: Học Toán ở trường

Bước 1. Bắt đầu với số học
Ở hầu hết các trường học, học sinh học số học ở bậc tiểu học. Số học bao gồm các khái niệm cơ bản về cộng, trừ, nhân và chia.
- Làm các câu hỏi thực hành. Làm đi làm lại các bài toán số học là cách tốt nhất để ghi nhớ những kiến thức cơ bản một cách chính xác. Hãy tìm phần mềm có thể cung cấp cho bạn nhiều loại bài toán Toán học khác nhau để giải quyết. Ngoài ra, hãy tìm các vấn đề với khung thời gian để cải thiện tốc độ của bạn.
- Bạn cũng có thể tìm các bài toán số học trực tuyến và bạn có thể tải các ứng dụng số học xuống thiết bị di động của mình.

Bước 2. Tiếp tục với phần tiền đại số
Bài tập này sẽ cung cấp cho bạn những yếu tố cơ bản mà bạn sẽ cần để giải các bài toán đại số sau này.
- Tìm hiểu về phân số và số thập phân. Bạn sẽ học cách cộng, trừ, nhân, chia phân số và số thập phân. Về phân số, bạn sẽ học cách trừ phân số và dịch các số kết hợp. Về số thập phân, bạn sẽ hiểu các giá trị vị trí và bạn sẽ có thể sử dụng số thập phân trong các bài toán của câu chuyện.
- Tìm hiểu về tỷ lệ, tỷ lệ và tỷ lệ phần trăm. Những khái niệm này sẽ giúp bạn học cách so sánh.
- Giới thiệu bản thân về hình học cơ bản. Bạn sẽ học các hình dạng và khái niệm 3D. Bạn cũng sẽ tìm hiểu các khái niệm như diện tích, chu vi, thể tích và diện tích bề mặt, cũng như thông tin về các đường thẳng và góc song song và vuông góc.
- Hiểu một số số liệu thống kê cơ bản. Trong giai đoạn tiền đại số, phần giới thiệu của bạn về số liệu thống kê thường bao gồm các hình ảnh như đồ thị, biểu đồ phân tán, biểu đồ âm mưu tem và biểu đồ.
- Tìm hiểu những điều cơ bản của đại số. Điều này bao gồm các khái niệm như giải phương trình đơn giản có chứa biến, tìm hiểu về các thuộc tính như tính chất phân phối, vẽ phương trình đơn giản và giải bất phương trình.
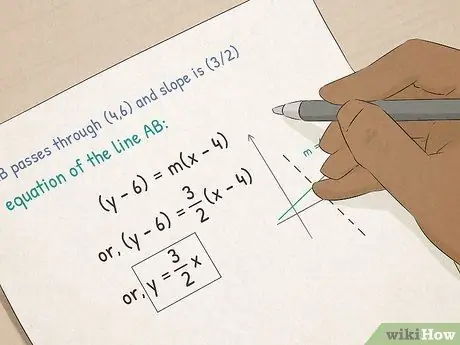
Bước 3. Học Đại số I
Trong năm đầu tiên học đại số, bạn sẽ học về các ký hiệu cơ bản có trong đại số. Bạn cũng sẽ học cách:
- Giải phương trình và bất phương trình chứa biến. Bạn sẽ học cách giải những bài toán này trên giấy và cách giải bằng hình ảnh.
- Giải quyết các vấn đề của câu chuyện. Bạn sẽ ngạc nhiên về bao nhiêu vấn đề hàng ngày bạn sẽ phải đối mặt trong tương lai đòi hỏi khả năng giải quyết các vấn đề câu chuyện đại số. Ví dụ: bạn sẽ sử dụng đại số để tìm ra lãi suất bạn kiếm được trên tài khoản ngân hàng hoặc khoản đầu tư của mình. Bạn cũng có thể sử dụng đại số để tính xem bạn nên đi trong bao lâu dựa trên tốc độ của ô tô.
- Làm việc với số mũ. Khi bạn bắt đầu giải phương trình đa thức (biểu thức chứa số và biến), bạn sẽ hiểu cách sử dụng số mũ. Điều này có thể sẽ bao gồm các bài tập với ký hiệu khoa học. Một khi bạn thành thạo số mũ, bạn có thể học cách cộng, trừ, nhân và chia các biểu thức đa thức.
- Giải các bài toán về căn bậc hai và căn bậc hai. Khi bạn nắm vững chủ đề này, bạn sẽ có thể ghi nhớ các bình phương của nhiều số. Bạn cũng sẽ có thể làm việc với các phương trình có căn bậc hai.
- Hiểu các hàm số và đồ thị. Trong đại số, bạn sẽ học về các phương trình đồ họa. Bạn sẽ học cách tính độ dốc của một đường, cách đặt phương trình ở dạng điểm-độ dốc và cách tính lát cắt x-và-y của một đường bằng cách sử dụng dạng chặn độ dốc.
- Tìm ra hệ phương trình. Đôi khi, bạn được cung cấp 2 phương trình khác nhau với các biến x và y, và bạn phải giải x hoặc y cho cả hai phương trình. May mắn thay, bạn sẽ học được rất nhiều thủ thuật để giải các phương trình này bao gồm vẽ đồ thị, thay thế và cộng.

Bước 4. Nghiên cứu hình học
Trong hình học, bạn sẽ học về các tính chất của đường thẳng, đoạn thẳng, góc và hình dạng.
- Bạn sẽ ghi nhớ một số định lý và hệ quả sẽ giúp bạn hiểu các quy tắc của hình học.
- Bạn sẽ học cách tính diện tích hình tròn, cách sử dụng định lý Pitago và cách tìm mối quan hệ giữa các góc và các cạnh của một tam giác đặc biệt.
- Bạn sẽ thấy nhiều câu hỏi về hình học trong các bài kiểm tra tiêu chuẩn hóa trong tương lai như SAT, ACT và GRE.
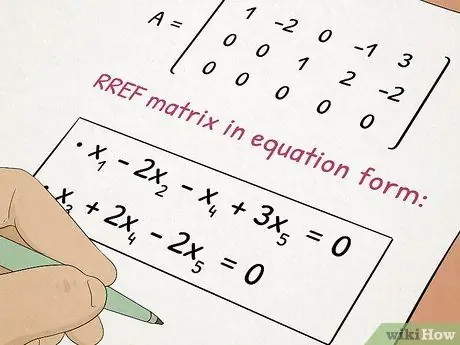
Bước 5. Học lớp Đại số II
Đại số II xây dựng dựa trên các khái niệm bạn đã học trong Đại số I đồng thời bổ sung vào các chủ đề phức tạp như phương trình bậc hai và ma trận.
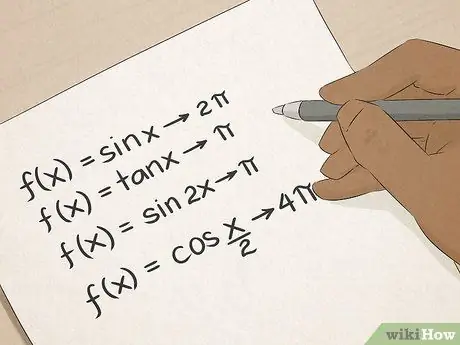
Bước 6. Nắm vững lượng giác
Bạn biết các thuật ngữ lượng giác: sin, cosine, tiếp tuyến, v.v. Lượng giác sẽ dạy cho bạn nhiều cách thực tế để tính góc và độ dài đoạn thẳng, và những kỹ năng này sẽ là vô giá đối với những người làm việc trong lĩnh vực xây dựng, kiến trúc, kỹ thuật hoặc khảo sát.
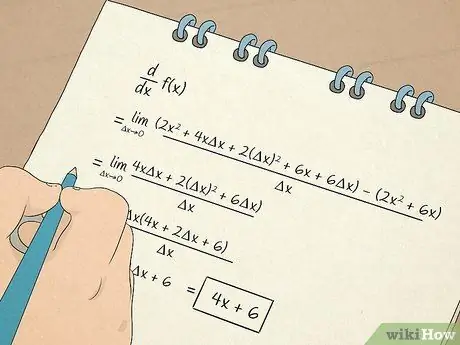
Bước 7. Thực hiện các phép tính giải tích
Giải tích nghe có vẻ đáng sợ, nhưng nó là một công cụ tuyệt vời để hiểu hành vi của các con số hoặc thế giới xung quanh bạn.
- Giải tích sẽ dạy bạn các hàm và giới hạn. Bạn sẽ thấy hành vi số của các hàm hữu ích bao gồm các hàm e ^ x và logarit.
- Bạn cũng sẽ học cách tính toán và làm việc với các công cụ phái sinh. Đạo hàm đầu tiên cung cấp cho bạn thông tin dựa trên hệ số góc của đường tiếp tuyến với một phương trình. Ví dụ: một phái sinh cho bạn biết tốc độ thay đổi của một cái gì đó trong một tình huống phi tuyến tính. Đạo hàm cấp hai sẽ cho bạn biết liệu hàm tăng hay giảm trong một khoảng thời gian nhất định, do đó bạn có thể xác định được độ tụ của một hàm.
- Tích phân sẽ dạy bạn cách tính diện tích dưới một đường cong cũng như thể tích của nó.
- Giải tích ở trường trung học thường kết thúc theo trình tự và trình tự. Mặc dù học sinh sẽ không thấy nhiều ứng dụng cho mạch, nhưng mạch rất quan trọng đối với những người nghiên cứu phương trình vi phân.
Phần 3/6: Các nguyên tắc cơ bản về toán - Bổ sung tổng thể

Bước 1. Bắt đầu với sự kiện "+1"
Thêm 1 vào một số sẽ đưa bạn đến số cao nhất trên trục số. Ví dụ: 2 + 1 = 3.
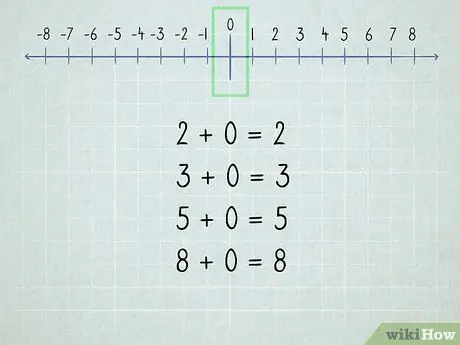
Bước 2. Hiểu số 0
Tất cả các số được thêm vào số 0 đều là cùng một số vì "số không" có nghĩa là "không có".

Bước 3. Học số kép
Nhiều số là một bài toán liên quan đến việc cộng hai số bằng nhau. Ví dụ, 3 + 3 = 6 là một ví dụ về phương trình liên quan đến nhiều số.

Bước 4. Sử dụng ánh xạ để tìm hiểu về các giải pháp bổ sung khác
Trong ví dụ dưới đây, bạn học bằng cách lập bản đồ điều gì sẽ xảy ra khi bạn thêm 3 với 5, 2 và 1. Hãy tự mình thử bài toán "thêm bằng 2".

Bước 5. Tiếp tục cho đến khi số lượng nhiều hơn 10
Học cách cộng 3 số với nhau để được một số lớn hơn 10.
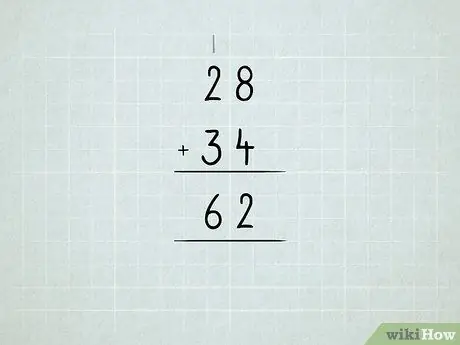
Bước 6. Cộng các số lớn hơn
Tìm hiểu về cách nhóm lại các đơn vị thành hàng chục, hàng chục thành hàng trăm, v.v.
- Cộng các số ở cột bên phải trước. 8 + 4 = 12, nghĩa là bạn có 1 số 10 và 2 số 1. Viết số 2 dưới cột đơn vị.
-
Viết số 1 vào cột hàng chục.
-
Cộng toàn bộ cột hàng chục.
Phần 4/6: Các nguyên tắc cơ bản về toán học - Chiến lược rút gọn

Bước 1. Bắt đầu với "lùi 1 chữ số
Trừ 1 cho một số sẽ đưa bạn trở lại 1 số. Ví dụ: 4 - 1 = 3.

Bước 2. Học phép trừ các số nhân đôi
Ví dụ, bạn thêm các số 5 + 5 để được 10. Chỉ cần viết ngược phương trình để có 10 - 5 = 5.
- Nếu 5 + 5 = 10 thì 10 - 5 = 5.
-
Nếu 2 + 2 = 4 thì 4 - 2 = 2.

Bước 3. Ghi nhớ gia đình dữ kiện
Như một ví dụ:
- 3 + 1 = 4
- 1 + 3 = 4
- 4 - 1 = 3
- 4 - 3 = 1

Bước 4. Tìm các số còn thiếu
Ví dụ: _ + 1 = 6 (câu trả lời là 5).

Bước 5. Ghi nhớ thực tế của phép trừ đến 20

Bước 6. Thực hành phép trừ số có 1 chữ số với số có 2 chữ số mà không cần mượn
Trừ các số ở cột hàng đơn vị và giảm các số ở cột hàng chục.
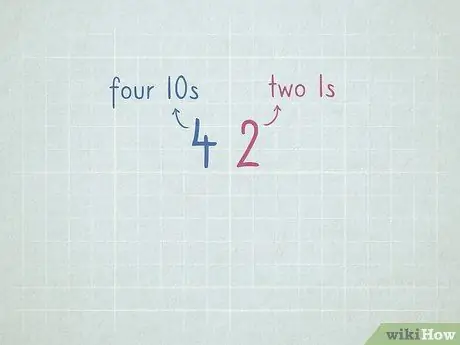
Bước 7. Thực hành giá trị vị trí để chuẩn bị cho phép trừ bằng cách đi vay
- 32 = 3 số 10 và 2 số 1.
- 64 = 6 số 10 và 4 số 1.
- 96 = _ số 10 và _ số 1.
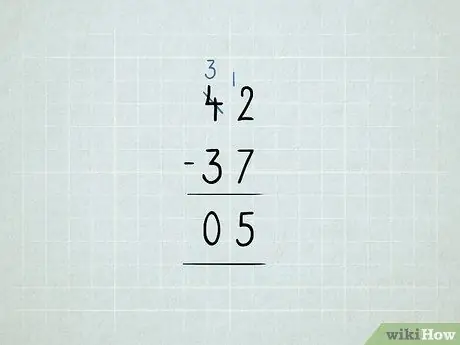
Bước 8. Trừ bằng cách đi vay
- Bạn muốn trừ 42 - 37. Bạn bắt đầu bằng cách thử trừ 2 - 7 trong cột đơn vị. Hóa ra, nó không hoạt động!
-
Mượn số 10 ở cột hàng chục và đặt nó vào cột hàng đơn vị. Bây giờ bạn có 3 chữ 10 thay vì 4 chữ 10. Bây giờ bạn có 12 chữ 1 thay vì 2 chữ 1.
-
Trừ đi cột đơn vị của bạn trước: 12 - 7 = 5. Sau đó, kiểm tra cột hàng chục. Vì 3 - 3 = 0 nên bạn không cần viết lại số 0. Câu trả lời của bạn là 5.
Phần 5/6: Các nguyên tắc cơ bản về toán - Phép nhân bậc thầy

Bước 1. Bắt đầu với số 1 và số 0
Tất cả các số được nhân với 1 đều giống như số chính nó. Bất kỳ số nào nhân với 0 cũng bằng không.

Bước 2. Học thuộc bảng cửu chương

Bước 3. Thực hành với các bài toán nhân một chữ số

Bước 4. Nhân số có 2 chữ số với số có 1 chữ số
- Nhân số dưới cùng bên phải với số trên cùng bên phải.
-
Nhân số dưới cùng bên phải với số trên cùng bên trái.
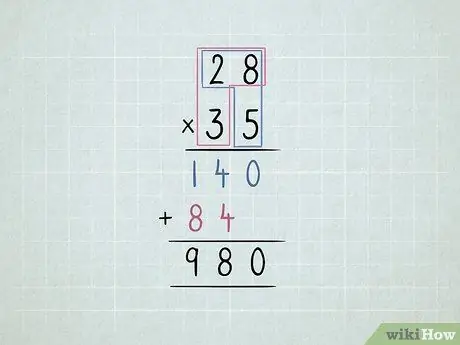
Bước 5. Nhân 2 số có 2 chữ số
- Nhân số dưới cùng bên phải với số trên cùng bên phải rồi nhân với số trên cùng bên trái.
-
Di chuyển hàng thứ hai sang trái một chữ số.
- Nhân số dưới cùng bên trái với số trên cùng bên phải rồi đến số trên cùng bên trái.
-
Cộng tất cả các cột.
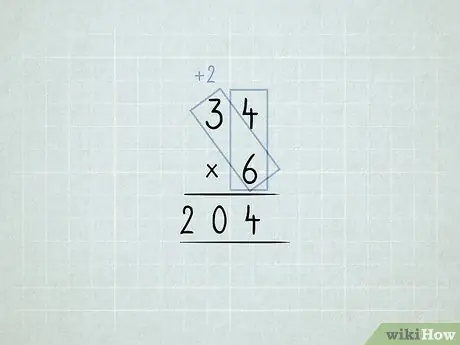
Bước 6. Nhân và nhóm lại các cột
- Bạn muốn nhân 34 x 6. Bạn bắt đầu bằng cách nhân cột đơn vị (4 x 6), nhưng bạn không thể có 24 số 1 trong cột đơn vị.
-
Lưu 4 số 1 trong cột đơn vị. Chuyển 2 số 10 sang cột hàng chục.
-
Nhân 6 x 3, được 18. Cộng 2 bạn đã chuyển, được 20.
Phần 6/6: Các nguyên tắc cơ bản về toán học - Tiết lộ các vấn đề về bộ phận

Bước 1. Suy nghĩ về phép chia đối lập với phép nhân
# * Nếu 4 x 4 = 16 thì 16/4 = 4.
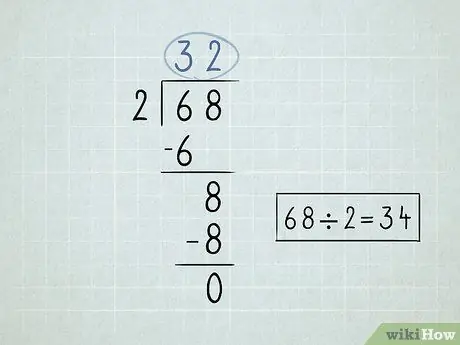
Bước 2. Viết ra bài toán chia của bạn
- Chia số ở bên trái của ký hiệu chia, hoặc số chia, cho số đầu tiên bên dưới ký hiệu số chia. Vì 6/2 = 3, bạn sẽ viết số 3 phía trên ký hiệu phép chia.
-
Nhân số phía trên ký hiệu phép chia với số bị chia. Đưa kết quả xuống dưới cùng của số đầu tiên dưới ký hiệu chia. Vì 3 x 2 = 6 nên bạn sẽ hạ số 6 xuống.
- Trừ 2 số bạn đã viết ra. 6 - 6 = 0. Bạn có thể để trống 0, vì bạn thường không bắt đầu các số bằng 0.
-
Đưa xuống số thứ hai nằm bên dưới ký hiệu chia.
- Chia số bạn mang xuống cho số chia. Trong trường hợp này, 8/2 = 4. Viết số 4 phía trên ký hiệu phép chia.
-
Nhân số trên cùng bên phải với số chia và hạ số đó xuống. 4 x 2 = 8.
-
Trừ các số đó. Phép trừ cuối cùng trả về 0, có nghĩa là bạn đã giải quyết được vấn đề. 68 x 2 = 34.

Bước 3. Cũng tính phần dư
Một số ước số không được chia hết thành các số khác. Nếu bạn đã hoàn thành phép trừ cuối cùng và bạn không còn số nào nữa để lấy ra, thì số cuối cùng là số dư.






