- Tác giả Jason Gerald [email protected].
- Public 2024-01-19 22:14.
- Sửa đổi lần cuối 2025-01-23 12:52.
Các quả bóng bi-a va vào nhau có độ đàn hồi hoàn hảo. Nghĩa là, động năng của chuyển động hầu như được bảo toàn hoàn toàn, và rất ít chuyển hóa thành nhiệt năng hoặc năng lượng khác. Điều này làm cho bida trở thành một môn thể thao thú vị được phân tích bằng toán học. Nếu bạn có toàn quyền kiểm soát cách bạn chọc vào quả bóng trắng và vị trí của nó, bạn sẽ luôn có thể dự đoán điều gì sẽ xảy ra.
Bươc chân
Phần 1/3: Dự đoán góc nảy của quả bóng trên đường ray
Bước 1. Nắm được quy luật phản xạ
Nhiều người chơi bi-a đã biết phép toán đơn giản này vì nó cần thiết mỗi khi họ muốn đánh bóng lên trên đường ray (các cạnh đệm trên bàn bi-a). Định luật này nói rằng góc tới của phản xạ bằng góc tới. Tức là, nếu quả bóng chạm vào đường ray một góc 30º thì góc nảy cũng sẽ là 30º.
Quy luật phản xạ ban đầu đề cập đến bản chất của ánh sáng. Thông thường, định luật này là "Góc tới bằng góc phản xạ."
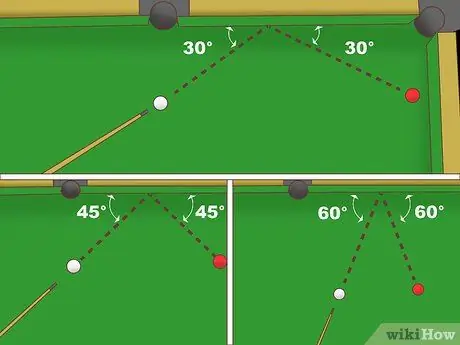
Bước 2. Đặt quả bóng màu trắng và quả bóng vật thể có cùng khoảng cách với đường ray
Trong kịch bản này, mục tiêu của bạn là ném quả bóng trắng lên đường ray và đánh quả bóng đối tượng. Bây giờ, hãy thử áp dụng các kỹ thuật hình học cơ bản sau:
- Vẽ một đường bóng từ quả bóng trắng vuông góc với đường ray. Đây là dòng đầu tiên.
- Sau đó, hãy tưởng tượng đường đi của phản xạ của quả bóng trắng đối với đường ray. Đường thẳng này là cạnh huyền (cạnh huyền) của một tam giác vuông được hình thành từ đường thẳng và đường ray đầu tiên.
- Bây giờ, hãy tưởng tượng quả bóng màu trắng bật ra khỏi đường ray và va vào quả bóng vật thể. Giả sử có một tam giác vuông thứ hai trên mặt cầu đối xứng với tam giác thứ nhất.
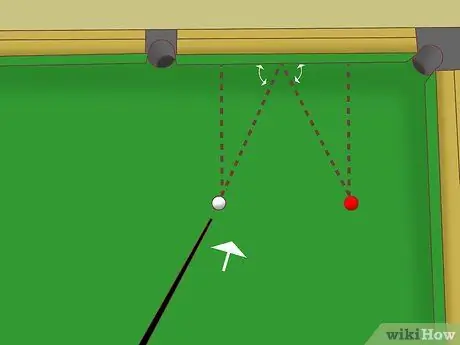
Bước 3. Chứng minh rằng hai tam giác này đồng dạng
Trong trường hợp này, chúng ta có thể sử dụng quy tắc "Side Angle". Nếu cả hai tam giác có hai góc bằng nhau và một cạnh bằng nhau (cùng cấu hình) thì hai tam giác đó đồng dạng. (Nói cách khác, hình dạng và kích thước giống nhau). Chúng ta có thể chứng minh xem hai tam giác trên bàn bi-a có thỏa mãn các điều kiện này hay không:
- Định luật phản xạ nói rằng hai góc giữa cạnh huyền và đường ray có cùng số đo.
- Cả hai đều là góc vuông nên mỗi góc có góc 90º.
- Vì hai quả bóng cách ray bằng nhau nên hai cạnh giữa quả bóng và thanh ray có cùng chiều dài.
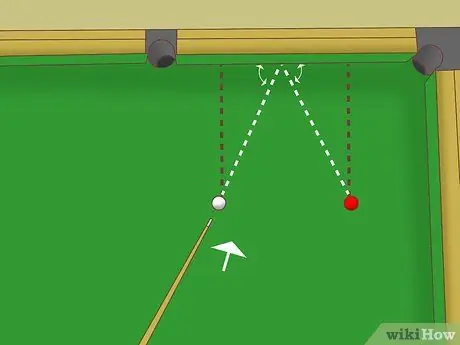
Bước 4. Nhắm vào điểm giữa của thanh ray
Vì hai tam giác này đồng dạng nên độ dài các cạnh trên thanh ray cũng bằng nhau. Tức là khoảng cách từ điểm nảy đến hai quả bóng là như nhau. Nhắm vào điểm giữa nếu viên bi trắng và viên bi vật thể cách đường ray bằng nhau.
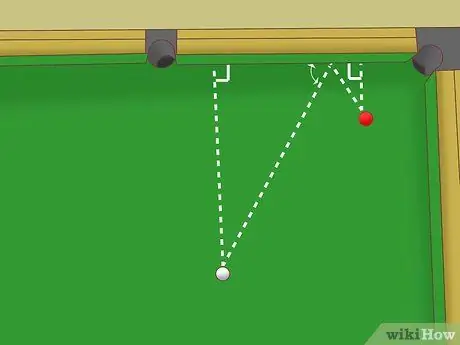
Bước 5. Sử dụng một tam giác tương tự nếu quả bóng màu trắng và quả bóng vật thể không có cùng khoảng cách từ đường ray
Cho biết khoảng cách của quả cầu màu trắng đến đường ray gấp đôi khoảng cách của quả cầu vật thể đến đường ray. Bạn vẫn có thể tưởng tượng hai tam giác vuông được tạo thành bởi đường đi lý tưởng của quả cầu màu trắng và sử dụng trực giác hình học của bạn để nhắm mục tiêu:
- Hai tam giác vẫn có các góc bằng nhau, nhưng độ dài các cạnh khác nhau. Tức là hai tam giác vẫn đồng dạng: hình dạng giống nhau, nhưng kích thước khác nhau.
- Vì quả bóng trắng ở xa đường ray gấp đôi nên hình tam giác thứ nhất lớn gấp đôi hình tam giác thứ hai.
- Tức là, cạnh ray của tam giác thứ nhất dài gấp đôi cạnh ray của tam giác thứ hai.
- Trong trường hợp này, nhắm vào một điểm trên đường ray ở khoảng cách từ quả cầu vật thể vì là hai lần.
Phần 2/3: Tính góc tác động của vật thể bi
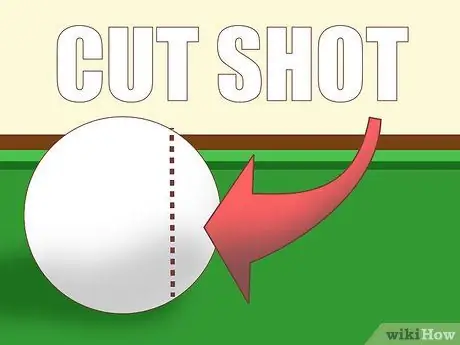
Bước 1. Tìm hiểu kiến thức cơ bản
Hầu hết các cú chọc trong bida là các cú đánh góc hoặc "cắt", có nghĩa là quả bóng trắng không đập trực tiếp vào đối tượng. Quả bóng đập càng "mỏng" thì góc đường đi của vật thể càng lớn, phụ thuộc vào quỹ đạo của quả bóng trắng.
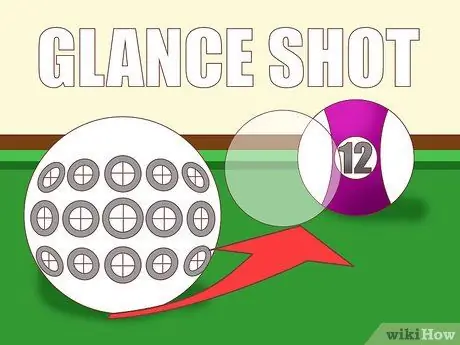
Bước 2. Ước tính mức độ đầy đủ của tác động
Một cách tốt để ước tính hiệu ứng này là theo dõi tác động đối với quỹ đạo dự kiến của quả bóng. Khi hai quả bóng va chạm, quả cầu màu trắng "chồng lên" quả cầu vật thể theo quan điểm của bạn bao nhiêu? Câu trả lời sẽ hiển thị mức độ "đầy" của quả bóng:
- Chết chồng lên nhau hoàn toàn. Bạn có thể nói mức độ "đầy đủ" là 1.
- Nếu viên bi trắng che được các viên bi của vật thì có nghĩa là sự va chạm của các viên bi là đầy đủ.
Bước 3. Ước tính góc dựa trên mức độ đầy đặn
Đồ thị của hai đại lượng này không hoàn toàn tuyến tính, nhưng đủ gần để bạn có thể ước lượng chúng bằng cách cộng thêm 15º mỗi khi bạn trừ đi mức đầy đủ. Nếu không, bạn có thể sử dụng các phép đo sau đây chính xác hơn:
- Tác động trực tiếp (độ đầy 1) dẫn đến góc cắt 0º. Quả cầu vật thể tiếp tục hoàn toàn đường đi của quả cầu màu trắng.
- Một cú va chạm đầy đủ sẽ làm cho quả cầu của vật thể đi một góc 14,5º.
- Một cú va chạm đầy đủ sẽ làm cho quả cầu của vật thể đi một góc 30º.
- Va chạm toàn phần sẽ làm quả cầu của vật chuyển động một góc 48, 6º.
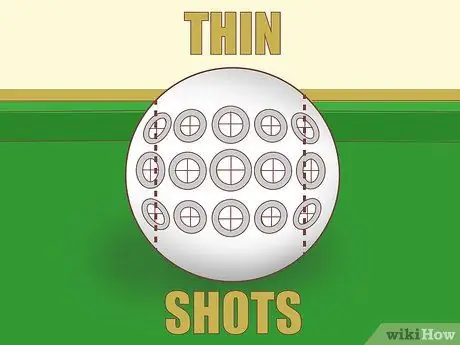
Bước 4. Hãy cẩn thận khi chụp mỏng
Nếu bạn muốn đánh quả bóng ở độ đầy ít hơn, rất khó để ước tính số lượng quả bóng được bao phủ. Hơn nữa, tác động của góc cắt rất mạnh nên một sai số nhỏ sẽ làm thay đổi rất nhiều góc tạo ra. Cú đánh tiếp tuyến này cần nhiều thực hành và hoạt động tốt khi bạn biết điểm mình đang nhắm tới. Nếu bạn có thể, hãy tìm một bức ảnh khác để chụp.
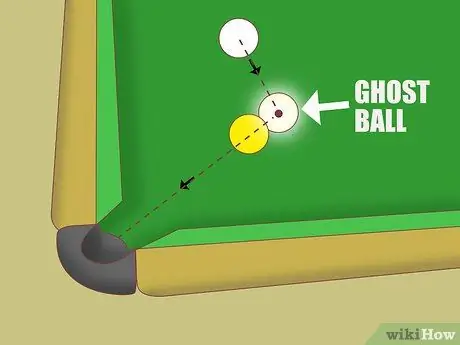
Bước 5. Hãy thử áp dụng phương pháp bóng ma để ngắm bắn
Nếu mô tả về toàn bộ tác động không giúp được bạn, hãy thử cách tiếp cận "bóng ma":
- Hãy tưởng tượng có một đường thẳng từ túi bàn đến tâm của quả cầu vật thể.
- Kéo dài đường này qua quả bóng vật thể một chút. Hãy tưởng tượng rằng có một “quả bóng ma” tại thời điểm này, đang ở trên dây và chạm vào quả cầu đối tượng.
- Để ném quả bóng vật thể vào túi, bạn cần nhắm vào tâm của “quả bóng ma”.
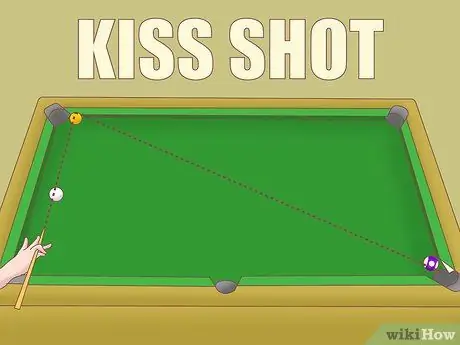
Bước 6. Áp dụng quy tắc chụp nụ hôn thứ ba
Một cú đánh bóng được thực hiện bằng cách đập một quả bóng trắng vào quả bóng A để nó nhắm tới và chạm quả bóng B. Nếu bạn đang chơi một trò chơi mà nụ hôn được phép, hãy ghi nhớ quy tắc này: nếu quả bóng A chạm vào đường ray, góc cắt bạn nhắm tới là góc tạo bởi ba quả bóng.
Ví dụ, nếu góc với mặt cầu A là đỉnh là 45º thì góc cắt là 15º. Quy tắc đầy đủ ở trên nói rằng góc này có thể được tạo ra với một va chạm đầy đủ
Phần 3/3: Sử dụng tiếng Anh (Side Twist)
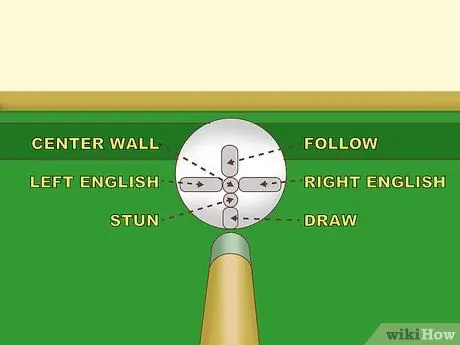
Bước 1. Hoàn thiện cú chọc của bạn trước
Ưu tiên hàng đầu nếu bạn muốn chơi bi-a một cách nghiêm túc. Tiếng Anh là một kỹ thuật rất hữu ích, nhưng tác dụng của nó rất phức tạp và bạn cần thực hành nó một cách nhất quán.
Bạn sẽ gặp khó khăn trong việc thu hẹp tầm ảnh hưởng của tiếng Anh nếu bạn không kiểm soát được các lực trượt và trượt. Tác động này được xác định bởi độ cao của điểm đẩy của quả bóng. Trượt bóng có thể được loại bỏ hoàn toàn bằng cách đánh vào một điểm bằng chiều dài giữa tâm và đỉnh của quả bóng, nhưng người chơi thường đánh ở một điểm khoảng cách này để đạt được tốc độ và khả năng kiểm soát tối ưu
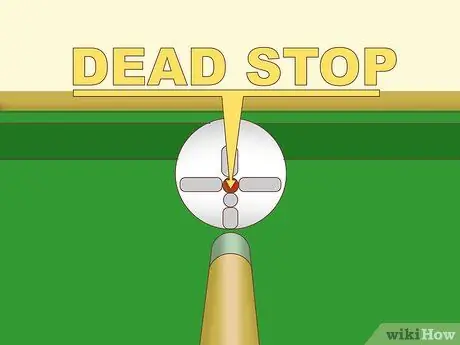
Bước 2. Tránh xa Anh khi bóng trắng có nguy cơ xâm nhập vào túi
Với điều kiện không có tiếng Anh, bóng trắng sẽ dừng lại hoàn toàn sau một cú va chạm trực tiếp hoàn hảo. Thực hành tác động trực tiếp bằng cách đánh chính xác vào tâm của trục dọc và trục ngang của quả bóng trắng. Khi bạn bị bóng trắng dừng lại hoàn toàn mỗi lần, bạn nên đủ kỹ năng để đưa tiếng Anh vào trò chơi.
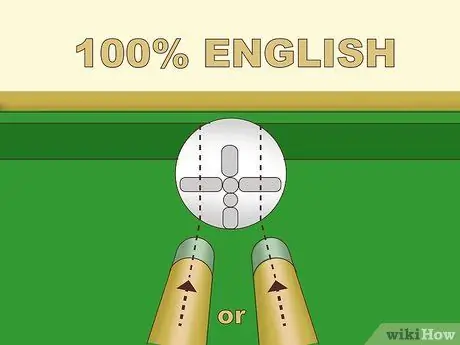
Bước 3. Thực hành các điểm mạnh tiếng Anh khác nhau
Có một số dạng tiếng Anh, nhưng bài viết này chỉ thảo luận về các dạng cơ bản. Nếu chiếc gậy chọc vào bên trái tâm của quả bóng, quả bóng sẽ quay dọc theo trục này; đây là "tiếng Anh trái". Khi quả bóng quay này chạm vào bề mặt, độ xoáy sẽ làm cho quả bóng quay sang trái nhiều hơn so với khi không có tiếng Anh. Ngược lại, chọc vào bên phải chính giữa bóng trắng sẽ làm bật lên "Anh quyền" và dội bóng xa hơn về phía bên phải. Bạn chọc càng xa tâm quả bóng, tác động càng lớn:
- Tiếng Anh 100% hoặc tối đa được thực hiện bằng cách chọc điểm giữa tâm và mép của quả bóng. Đây là khoảng cách chọc khe tối đa để có được một cú chọc khe với sai số tối thiểu.
- Tiếng Anh 50% được thực hiện bằng cách chọc vào điểm giữa của điểm cực đại và tâm của quả bóng (¼ khoảng cách giữa tâm đến mép của quả bóng).
- Bạn có thể sử dụng tỷ lệ phần trăm tiếng Anh bằng cách chọc vào các điểm khác nhau giữa tâm và điểm tối đa của bóng trắng.
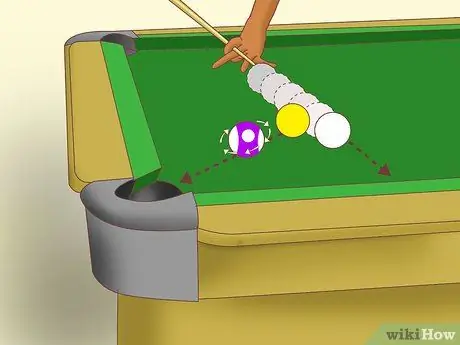
Bước 4. Hiểu về cách chuyển số
Khi hai quả bóng va chạm, quả cầu vật thể bắt đầu quay trên một trục nhất định, theo góc của cú đánh và lượng tiếng Anh thu được. Nếu bạn có thể đạt được "bánh răng", chuyển động quay này xảy ra dọc theo trục chuyển động. Nói cách khác, chuyển động của quả cầu vật thể không bị ảnh hưởng bởi chuyển động quay. Quả bóng sẽ trượt dọc theo “đường tâm” hoặc đường kẻ giữa tâm của hai quả bóng khi va chạm.
Thuật ngữ này xuất phát từ sự tương tự của hai bánh răng hoạt động trơn tru với nhau và truyền chuyển động một cách hoàn hảo
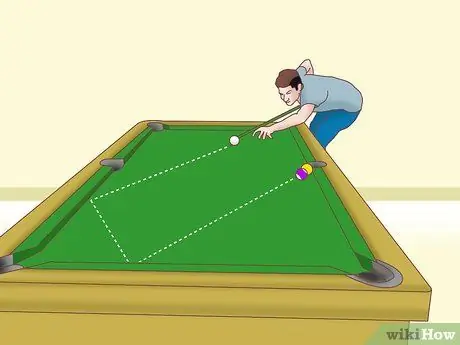
Bước 5. Điều chỉnh tiếng Anh để đạt được thành công trong tất cả các phần
Khi bạn đã sút vào một góc bằng cách sử dụng phương pháp tiếp cận "bóng đầy đủ" hoặc "bóng ma", bạn nên đảm bảo rằng bóng đối tượng không quay một cách kỳ lạ và làm hỏng cú đánh của bạn. Đây là biểu đồ có thể giúp bạn tìm góc phù hợp và tiếng Anh. Tất cả các số bên dưới đều là "tiếng Anh bên ngoài" có nghĩa là bạn di chuyển gậy bên cạnh quả bóng trắng xa hơn quả bóng đối tượng.
- Nếu góc cắt là 15º, hãy sử dụng tiếng Anh lớn hơn 20% một chút. (Hãy nhớ rằng, góc cắt là góc giữa đường đi ban đầu của bóng trắng và đường đi của bóng của vật thể.)
- Nếu góc cắt là 30º, hãy sử dụng tiếng Anh ở mức 40%.
- Nếu góc cắt là 45º, sử dụng 55% tiếng Anh.
- Nếu góc cắt là 60º, sử dụng tiếng Anh ở mức 70%.
- Khi góc cắt tiếp cận 90º, hãy tăng tiếng Anh lên 80%.
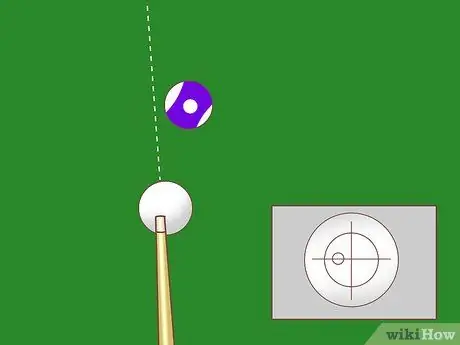
Bước 6. Biết ảnh hưởng của tác động mà không cần gài số
Nếu bạn sử dụng tiếng anh ít hơn trong số nhiều "bánh răng" ở bước cuối cùng, quả cầu màu trắng sẽ dịch chuyển về phía trước trong khi va chạm, và đường xoắn bên chuyển sang quả cầu vật thể. Khi đó, viên bi vật thể sẽ di chuyển nhẹ sang phải so với góc cắt ước tính. Nếu tiếng Anh của bạn không chỉ là sang số, viên bi vật thể sẽ di chuyển một chút sang bên trái của góc cắt ước tính.
- Hiệu ứng này được gọi là cú ném gây ra bởi vết cắt: góc của vết cắt làm thay đổi đường xoắn làm cho quả bóng lăn hơi lệch hướng.
- Bạn có thể sử dụng kỹ thuật này để thực hiện những bức ảnh tưởng chừng như không thể. Nếu cú sút duy nhất của bạn hơi quá xa về phía bên phải, hãy tăng khả năng tiếng Anh của bạn để đưa bóng vào túi.
Lời khuyên
- Nếu quả bóng vật thể bị kẹt vào thanh ray và bạn cần lăn nó theo đường ray về phía túi, hãy luôn đập vào thanh ray trước khi chạm vào quả cầu vật thể. Do đó, quả bóng màu trắng tạo đà cho đường ray, thay vì hướng về phía nó. (Nếu góc tác động vượt quá 45º, bạn sẽ cần sử dụng tiếng Anh.)
- Góc va chạm giữa hai quả cầu càng lớn thì động lượng truyền càng nhỏ. Điều này có nghĩa là bạn sẽ cần phải chọc mạnh hơn một chút để có những vết cắt mỏng (vết nứt ở các góc cực).
- Sau va chạm, góc giữa đường đi của bi trắng và đường đi của vật phải luôn bằng 90º. Sử dụng kiến thức này để ngăn bóng trắng xâm nhập vào túi. Lưu ý rằng xoắn quá mức có thể phá vỡ quy tắc này và các quả bóng có khối lượng khác nhau (ví dụ: trên bàn bi-a thông thường trong quán cà phê).






