- Tác giả Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-19 22:14.
- Sửa đổi lần cuối 2025-01-23 12:52.
Phép trừ chỉ đơn giản là trừ một số với một số khác. Thật dễ dàng để trừ một số nguyên với một số khác, nhưng phép trừ có thể phức tạp nếu bạn đang trừ phân số hoặc số thập phân. Khi bạn hiểu phép trừ, bạn sẽ có thể sử dụng các khái niệm toán học phức tạp hơn và có thể cộng, nhân và chia các số dễ dàng hơn.
Bươc chân
Phương pháp 1/6: Trừ các số nguyên lớn bằng cách đi vay

Bước 1. Viết ra một số lớn
Ví dụ, bạn muốn giải quyết 32 - 17. Trước tiên hãy viết ra 32.

Bước 2. Viết số nhỏ hơn ngay bên dưới nó
Đảm bảo rằng bạn đặt các giá trị hàng chục và hàng đơn vị vào các cột chính xác, sao cho 3 trong số 32 nằm ngay trên 1 trên 17 và 2 của 32 nằm ngay trên 7 trên 17.
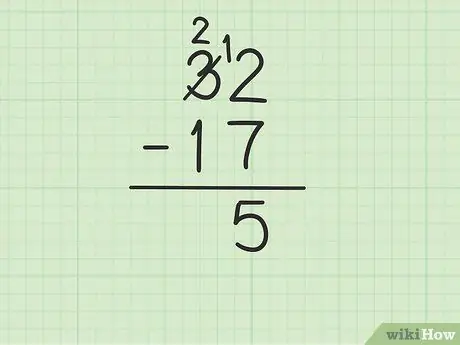
Bước 3. Trừ số trên cùng trong cột đơn vị với số ở dưới cùng
Tuy nhiên, điều này có thể trở nên phức tạp nếu số dưới cùng lớn hơn số trên cùng. Trong trường hợp này, 7 lớn hơn 2. Đây là những gì bạn phải làm:
- Bạn phải vay từ số 3 trong số 32 (còn được gọi là nhóm), để chuyển 2 thành 12.
- Hãy gạch số 3 ra số 32 và thay bằng số 2, trong khi số 2 trở thành 12.
- Bây giờ bạn có thể trừ 12 - 7, được bằng 5. Viết 5 dưới hai số bạn đang trừ sao cho chúng ở cột đơn vị của hàng mới.
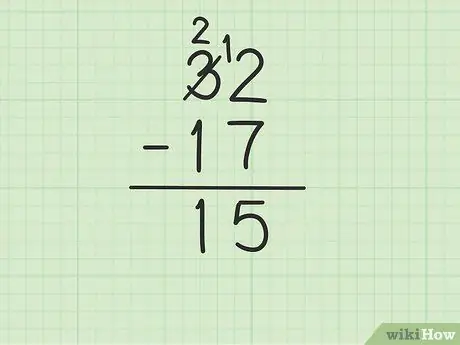
Bước 4. Trừ số trên cùng ở cột hàng chục với số dưới cùng
Hãy nhớ 3 đã trở thành 2. Bây giờ trừ 1 từ 17 từ 2 ở trên để được (2-1) 1. Viết 1 vào bên dưới, ở cột hàng chục, bên trái của 5 ở cột đơn vị. Bạn viết 15. Tức là, 32 - 17 = 15.
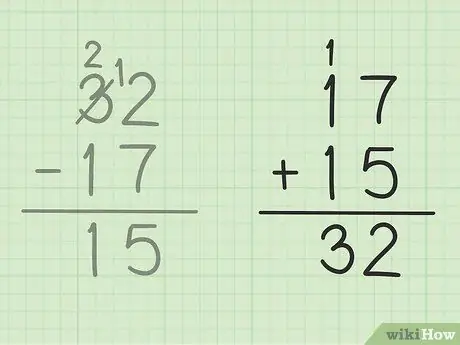
Bước 5. Kiểm tra công việc của bạn
Nếu bạn muốn chắc chắn rằng bạn đã trừ hai số một cách chính xác, thì tất cả những gì bạn phải làm là cộng câu trả lời của mình với số nhỏ hơn để tạo thành một số lớn. Trong bài toán này, bạn phải thêm câu trả lời của bạn, 15 vào số nhỏ hơn của phép trừ, 17. 15 + 17 = 32, để câu trả lời của bạn là đúng. An toàn!
Phương pháp 2/6: Trừ các số nguyên nhỏ
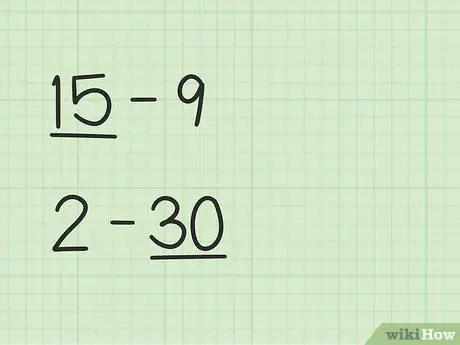
Bước 1. Tìm số lớn hơn
Các bài toán như 15 -9 sẽ có cách giải khác với 2 - 30.
- Trong các câu hỏi từ câu 15 - 9, số thứ nhất là 15 lớn hơn số thứ hai là 9.
- Trong câu hỏi 2 - 30, số thứ hai là 30 lớn hơn số thứ nhất là 2.
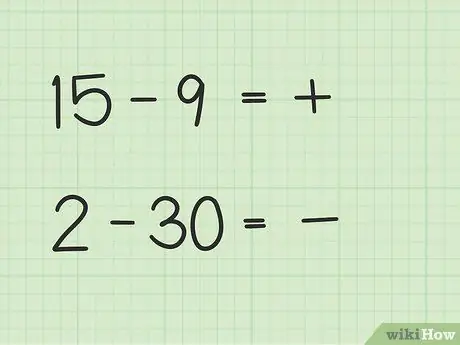
Bước 2. Quyết định xem câu trả lời của bạn là tích cực hay tiêu cực
Nếu số đầu tiên lớn hơn, câu trả lời là dương. Nếu số thứ hai lớn hơn, câu trả lời là số âm.
- Trong câu hỏi đầu tiên, 15-9, câu trả lời của bạn là dương vì số thứ nhất lớn hơn số thứ hai.
- Trong câu hỏi thứ hai, 2 - 30, câu trả lời của bạn là âm vì số thứ hai lớn hơn số thứ nhất.
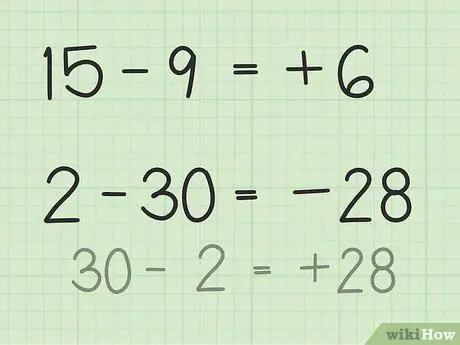
Bước 3. Tìm hiệu giữa hai số
Để trừ hai số, bạn phải tưởng tượng sự khác biệt giữa hai số và tính các số giữa chúng.
- Đối với các câu hỏi từ 15 đến 9, hãy tưởng tượng một xấp gồm 15 chip poker. Vứt bỏ 9 chip và chỉ còn 6. Vì vậy, 15 - 9 = 6. Bạn cũng có thể hình dung một dãy số. Nghĩ về các số từ 1 đến 15, sau đó loại bỏ hoặc trả lại 9 đơn vị để bạn nhận được 6.
- Đối với câu hỏi 2 - 30, cách dễ nhất để giải quyết điều này là đảo ngược số và làm cho kết quả âm sau khi trừ. Vì vậy, 30 - 2 = 28 nên 28 và 30 có hiệu là 2. Bây giờ, hãy làm cho kết quả âm vì bạn đã xác định rằng câu trả lời là âm vì số thứ hai lớn hơn số thứ nhất. Vì vậy, 2 - 30 = -28.
Phương pháp 3/6: Trừ số thập phân
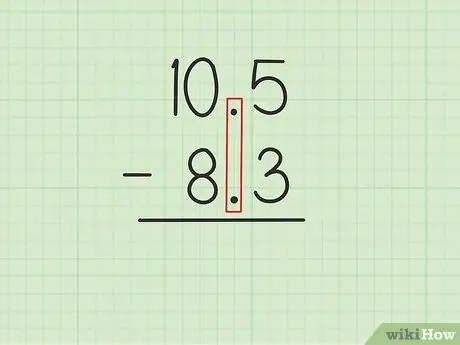
Bước 1. Viết số lớn hơn số nhỏ hơn với các dấu thập phân thẳng hàng
Giả sử bạn muốn giải các bài toán sau: 10, 5 - 8, 3. Viết 10, 5 trên 8, 3 sao cho các dấu thập phân của hai số đó song song với nhau., 5 trên 10, 5 phải ở trên, 3 trong 8, 3 và 0 của 10, 5 phải trên 8 trên 8, 3.
Nếu bạn gặp khó khăn do hai số không có cùng số sau dấu thập phân, hãy viết số 0 vào ô trống cho đến khi tổng các số bằng nhau. Ví dụ, bài toán là 5, 32 - 4, 2, bạn có thể viết là 5, 32 - 4, 2 0. Điều này sẽ không thay đổi giá trị của số thứ hai, nhưng sẽ làm cho việc trừ hai số dễ dàng hơn.

Bước 2. Trừ số trên cùng ở cột hàng chục với số dưới đây
Trong trường hợp này, bạn phải trừ 3 với 5. 5 - 3 = 2, vì vậy bạn phải viết 2 dưới 3 của 8, 3.
Hãy chắc chắn rằng bạn đã đặt một dấu chấm thập phân trong câu trả lời để nó được viết, 2

Bước 3. Trừ số bên trên cột đơn vị với số bên dưới nó
Bạn phải trừ 8 với 0. Mượn 1 ở phần chục để đổi 0 thành 10 và trừ 10 - 8 để được 2. Bạn cũng có thể đếm 10 - 8 mà không cần mượn vì không có số nào ở cột hàng chục thứ hai. Viết câu trả lời dưới 8, bên trái dấu thập phân.

Bước 4. Viết ra kết quả cuối cùng của bạn
Kết quả cuối cùng của bạn là 2, 2.

Bước 5. Kiểm tra công việc của bạn
Nếu bạn muốn đảm bảo phép trừ số thập phân của mình là chính xác, tất cả những gì bạn phải làm là cộng câu trả lời của mình với số nhỏ hơn để tạo thành số lớn hơn. 2, 2 + 8, 3 = 10, 5, vậy là bạn đã hoàn thành.
Phương pháp 4/6: Trừ phân số

Bước 1. Căn giữa mẫu số và tử số của phân số
Giả sử bạn muốn giải các bài toán 13/10 - 3/5. Viết bài toán sao cho hai tử số là 13 và 3 và hai mẫu số là 10 và 5 đối nhau. Hai số này được phân tách bằng dấu trừ. Điều này sẽ giúp bạn hình dung vấn đề và giải quyết nó dễ dàng hơn.

Bước 2. Tìm mẫu số chung nhỏ nhất
Mẫu số chung nhỏ nhất là số nhỏ nhất có thể chia cho hai số. Trong ví dụ này, bạn phải tìm mẫu số chung nhỏ nhất chia hết cho 10 và 5. Bạn sẽ thấy rằng 10 là mẫu số chung nhỏ nhất cho cả hai số vì 10 chia hết cho 10 và 5.
Lưu ý rằng mẫu số chung nhỏ nhất của hai số không phải lúc nào cũng là một trong số chúng. Ví dụ, mẫu số chung nhỏ nhất của 3 và 2 là 6 vì 6 là số nhỏ nhất có thể chia cho hai số
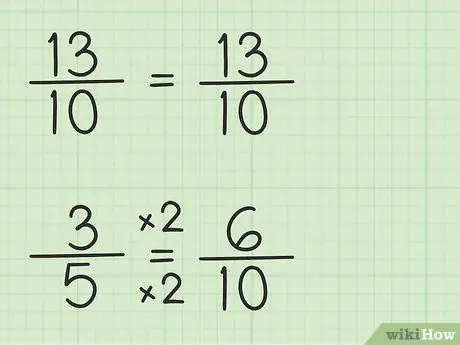
Bước 3. Viết các phân số cùng mẫu số
Phân số 13/10 có thể viết như vậy vì mẫu số là 10, mẫu số chung nhỏ nhất là 10 nhân 1. Tuy nhiên, phân số 3/5 phải viết lại vì mẫu số là 5, mẫu số chung nhỏ nhất. Nhân là 10, nhân 2. Vậy phân số 3/5 phải nhân với 2/2 mới được mẫu số 10 nên 3/5 x 2/2 = 6/10. Bạn đã tìm được phân số tương đương. 3/5 tương đương với 6/10 mặc dù 6/10 cho phép bạn trừ số đầu tiên, 13/10.
Viết một câu hỏi mới như sau: 13/10 - 6/10
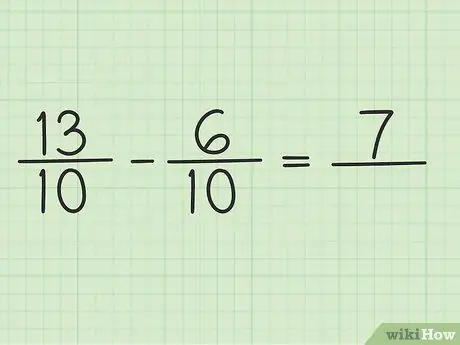
Bước 4. Trừ tử số cho hai số
Chỉ cần trừ 13 - 6 để kết quả là 7. Bạn không thể thay đổi mẫu số của phân số.
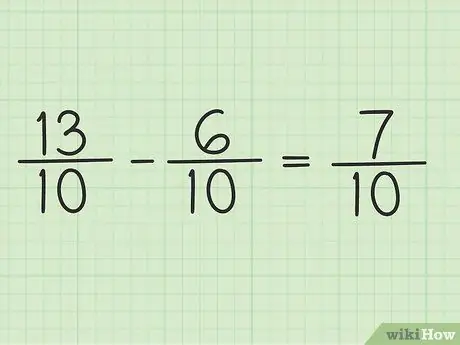
Bước 5. Viết tử số mới trên cùng mẫu số để có kết quả cuối cùng
Tử số mới là 7. Cả hai phân số đều có mẫu số là 10. Kết quả cuối cùng của bạn là 7/10.
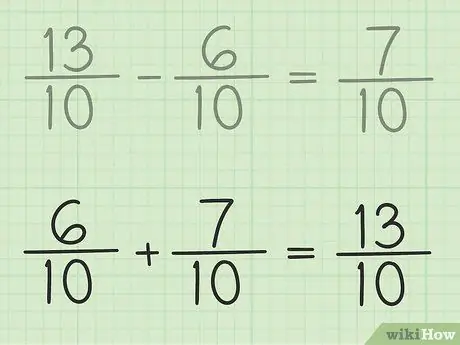
Bước 6. Kiểm tra công việc của bạn
Nếu bạn muốn chắc chắn rằng bạn đang trừ phân số một cách chính xác, chỉ cần cộng câu trả lời của bạn và phân số nhỏ hơn để kết quả là phân số lớn hơn. 7/10 + 6/10 = 13/10. Mọi chuyện đã kết thúc rồi.
Phương pháp 5/6: Trừ các phân số khỏi các số nguyên

Bước 1. Viết ra vấn đề
Ví dụ, giả sử bạn muốn giải bài toán sau: 5 -. Viết nó ra.
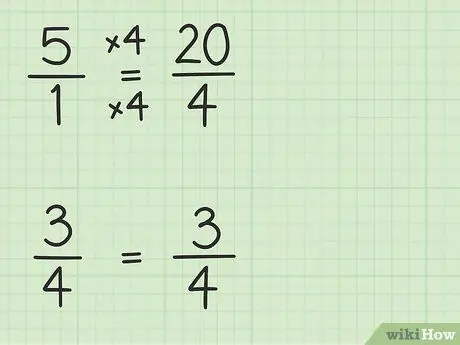
Bước 2. Chuyển các số nguyên thành phân số có cùng mẫu số với các phân số khác
Bạn sẽ chuyển 5 thành một phân số có mẫu số là 4 để có thể trừ hai số. Vì vậy, bạn cần nghĩ 5 là một phần của 5/1. Sau đó, bạn có thể nhân tử số và mẫu số của phân số mới với 4 để làm cho mẫu số của hai số đó bằng nhau. Vậy 5/1 x 4/4 = 20/4. Phân số này bằng 5, nhưng cho phép bạn trừ hai số.
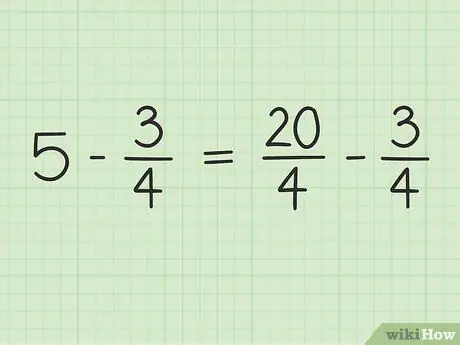
Bước 3. Viết lại vấn đề
Bài toán mới có thể viết như sau: 20/4 - 3/4.
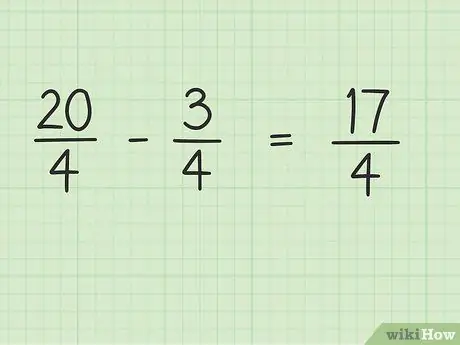
Bước 4. Trừ tử số của phân số, còn mẫu số thì giữ nguyên
Bây giờ, chỉ cần trừ 20 cho 3 để có kết quả cuối cùng. 20 - 3 = 17 nên 17 là tử số mới. Bạn có thể để nguyên mẫu số.
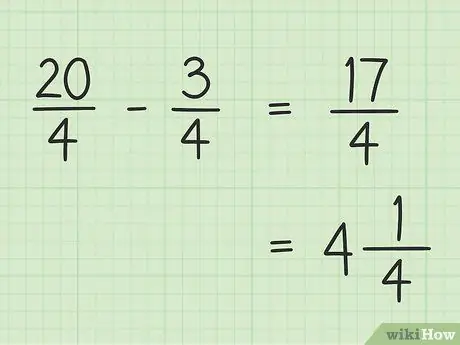
Bước 5. Viết ra kết quả cuối cùng của bạn
Kết quả cuối cùng của bạn là 17/4. Nếu bạn muốn viết nó dưới dạng hỗn số, hãy chia 17 cho 4 để được kết quả là 4 và số dư là 1, sao cho 17/4 cuối cùng của bạn bằng 4.
Phương pháp 6/6: Trừ các biến
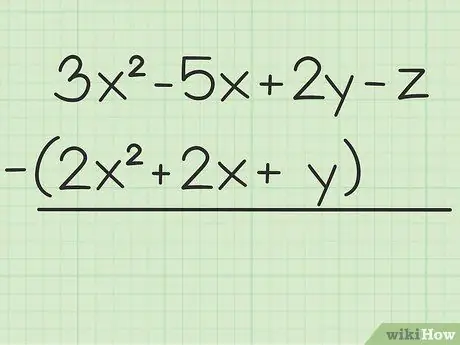
Bước 1. Viết ra vấn đề bạn muốn giải quyết
Ví dụ câu hỏi sau: 3x2 - 5x + 2y - z - (2x2 + 2x + y). Viết tập hợp các biến đầu tiên so với tập thứ hai.
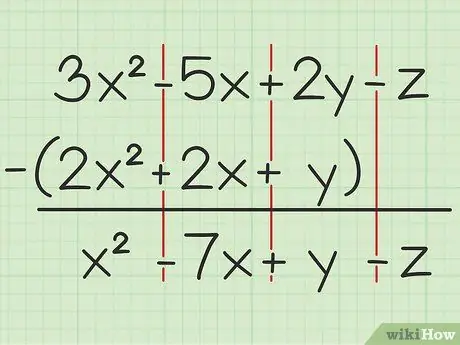
Bước 2. Trừ các biến giống nhau
Nếu bạn gặp một biến, bạn chỉ có thể cộng hoặc trừ cùng một biến và được viết với cùng một mức độ bình phương. Điều đó có nghĩa là bạn có thể trừ 4x2 từ 7x2, nhưng không thể trừ 4x cho 4y. Vì vậy, bạn có thể chia nhỏ vấn đề như sau:
- 3x2 - 2x2 = x2
- -5x - 2x = -7x
- 2y - y = y
- -z - 0 = -z
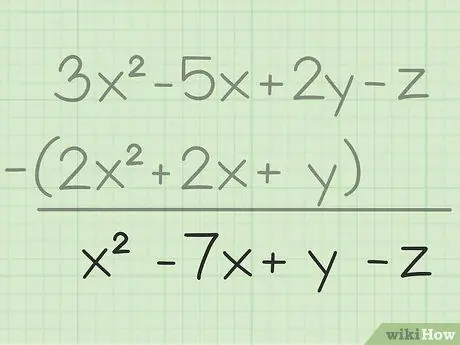
Bước 3. Viết ra kết quả cuối cùng của bạn
Bạn đã trừ tất cả các biến giống nhau, tất cả những gì bạn phải làm là viết kết quả cuối cùng sẽ chứa tất cả các biến bạn đã trừ. Đây là kết quả cuối cùng:






