Căn bậc hai của một số rất dễ tìm nếu câu trả lời là một số nguyên. Nếu câu trả lời không phải là số nguyên, bạn có thể thực hiện một loạt quy trình để lấy căn bậc hai, ngay cả khi bạn không sử dụng máy tính. Để làm được điều đó, bạn cần hiểu những điều cơ bản về phép nhân, phép cộng và phép chia.
Bươc chân
Phương pháp 1/3: Tìm Căn bậc hai của một số nguyên
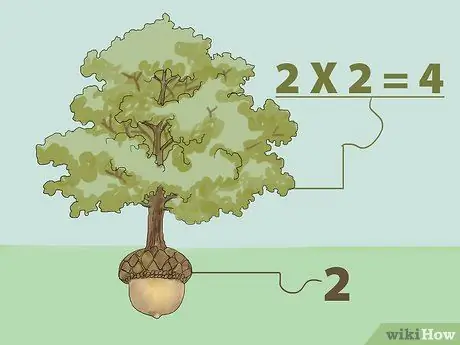
Bước 1. Tìm căn bậc hai hoàn hảo bằng cách nhân
Căn bậc hai của một số là một số khi nhân với chính nó sẽ trả về số ban đầu. Nói cách khác: "Ta có thể nhân với chính nó với số nào để được số ta muốn?"
- Ví dụ, căn bậc hai của 1 là 1 vì 1 nhân với 1 được 1 (1X1 = 1). Như vậy, căn bậc hai của 4 là 2 vì 2 nhân với 2 được 4 (2X2 = 4). Hãy nghĩ về khái niệm căn bậc hai như một cái cây. Một cái cây mọc lên từ hạt giống. Vì vậy, một cái cây lớn hơn một hạt giống, nó phát triển từ một hạt giống là gốc của nó. Từ ví dụ trên, 4 là cây, và 2 là hạt.
- Vì vậy, căn bậc hai của 9 là 3 (3X3 = 9), của 16 là 4 (4X4 = 16), của 25 là 5 (5X5 = 25), của 36 là 6 (6X6 = 36), của 49 là 7 (7X7 = 49), từ 64 là 8 (8X8 = 64), từ 81 là 9 (9X9 = 81) và từ 100 là 10 (10X10 = 100).
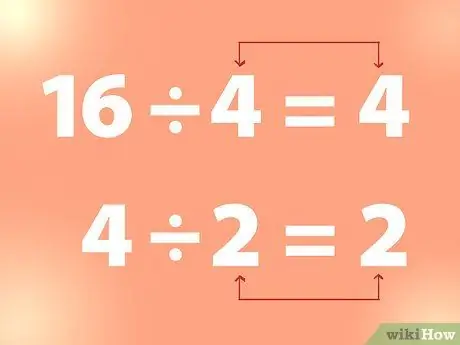
Bước 2. Sử dụng phép chia liên tục để tìm căn bậc hai
Để tìm căn bậc hai của một số nguyên, bạn có thể chia số nguyên cho một số cho đến khi bạn nhận được một số bằng số chia.
- Ví dụ: 16 chia cho 4 là 4. Và 4 chia cho 2 là 2, v.v. Như vậy, từ ví dụ trên, 4 là căn bậc hai của 16 và 2 là căn bậc hai của 4.
- Căn bậc hai hoàn hảo không có phân số hoặc số thập phân vì chúng là số nguyên.
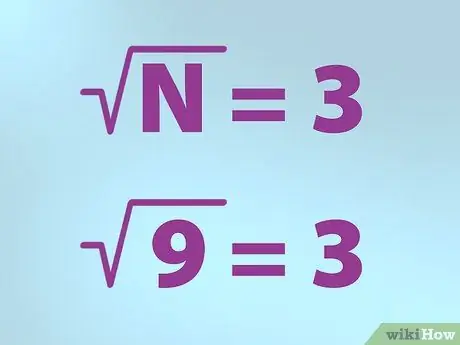
Bước 3. Sử dụng ký hiệu chính xác cho căn bậc hai
Các nhà toán học sử dụng một ký hiệu đặc biệt để biểu diễn căn bậc hai. Hình dạng giống như một dấu kiểm với dấu cộng ở trên cùng bên phải.
- N bằng số mà bạn muốn tìm căn bậc hai. N được đặt dưới dấu kiểm.
- Vì vậy, nếu bạn muốn tìm căn bậc hai của 9, hãy viết một công thức bằng cách đặt "N" (9) bên trong một dấu kiểm (ký hiệu "root") sau đó viết một dấu bằng và theo sau là 3. Nó có nghĩa là "căn bậc hai của 9 bằng 3”.
Phương pháp 2/3: Tìm căn bậc hai của một số khác
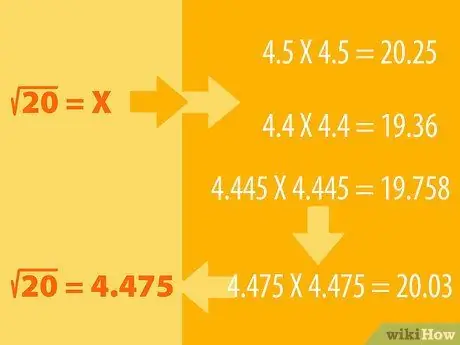
Bước 1. Đoán và thực hiện quá trình loại bỏ
Rất khó để tìm căn bậc hai của một số không nguyên. Tuy nhiên, điều đó không có nghĩa là không thể.
- Ví dụ, giả sử bạn muốn tìm căn bậc hai của 20. Chúng ta biết rằng 16 là một hình vuông hoàn hảo có căn bậc hai là 4 (4X4 = 16). Khi đó 25 căn bậc hai là 5 (5X5 = 25), vì vậy căn bậc hai của 20 phải nằm giữa hai căn.
- Bạn có thể đoán rằng căn bậc hai của 20 là 4,5. Bây giờ hãy bình phương 4,5 để xem kết quả. Tức là, chúng ta nhân 4, 5 với chính nó: 4, 5X4, 5. Xem câu trả lời là lớn hơn hay nhỏ hơn 20. Nếu dự đoán của bạn quá xa, hãy thử một số khác (ví dụ: 4, 6 hoặc 4, 4) và điều chỉnh dự đoán tương ứng. bạn cho đến khi bạn nhận được số 20.
- Ví dụ: 4, 5X4, 5 = 20, 25, vì vậy theo logic chúng ta phải tìm một số nhỏ hơn, có thể là 4, 4. 4, 4X4, 4 = 19, 36. Vì vậy, căn bậc hai của 20 phải nằm giữa 4, 5 và 4, 4. Thử với 4, 445X4, 445. Kết quả là 19, 758. Kết quả ngày càng gần. Tiếp tục thử với các số khác cho đến khi bạn nhận được 4, 475X4, 475 = 20, 03. Làm tròn lại, số đó bằng 20.
Bước 2. Sử dụng quy trình tính trung bình
Quá trình này cũng bắt đầu bằng cách tìm hai hình vuông hoàn hảo gần nhất có hai bên là số.
- Sau đó chia số đó cho một trong các căn bậc hai hoàn hảo. Lấy câu trả lời, sau đó tìm trung bình cộng giữa số đó và số bạn muốn tìm căn (bạn có thể tìm trung bình bằng cách cộng hai số với nhau và chia cho hai). Sau đó chia số ban đầu cho số trung bình thu được. Bước cuối cùng, tìm giá trị trung bình của các kết quả với giá trị trung bình được tính lần đầu.
- Nghe có vẻ phức tạp? Sẽ dễ dàng hơn nếu được đưa ra một ví dụ. Ví dụ, 10 nằm giữa hai hình vuông hoàn hảo 9 (3X3 = 9) và 16 (4X4 = 16). Căn bậc hai của cả hai số là 3 và 4. Vì vậy, chia 10 cho số đầu tiên được 3. Kết quả là 3, 33. Bây giờ hãy tìm trung bình cộng của 3 và 3, 33 bằng cách cộng chúng với nhau và chia cho 2. Kết quả là 3, 1667 Bây giờ chia 10 cho 3,1667 được kết quả là 3,1579 Sau đó tìm trung bình cộng của 3,1579 và 3,1667 bằng cách cộng chúng lại và chia cho 2. Kết quả là 3,1623.
- Kiểm tra kết quả của bạn bằng cách nhân câu trả lời (trong ví dụ này là 3, 1623) với chính nó. Kết quả của 3,1623 nhân với 3,1623 được 10,001.
Phương pháp 3/3: Bình phương số âm
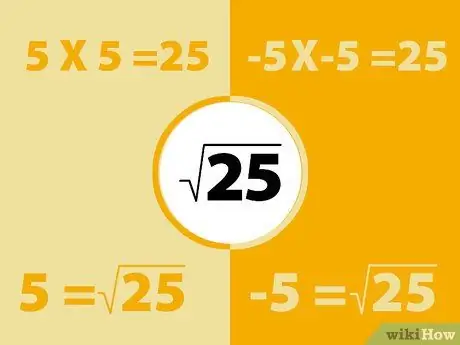
Bước 1. Số âm vuông bằng cách sử dụng cùng một phương pháp
Hãy nhớ rằng thời gian tiêu cực là tiêu cực là tích cực. Vì vậy, bình phương của một số âm sẽ tạo ra một số dương.
- Ví dụ, -5X-5 = 25. Tuy nhiên, hãy nhớ rằng 5x5 = 25. Vì vậy, căn bậc hai của 25 có thể là -5 hoặc 5. Về cơ bản mọi số đều có hai căn bậc hai.
- Tương tự, 3X3 = 9 và -3X-3 = 9, do đó các căn bậc hai của 9 là 3 và -3. Căn bậc hai dương được gọi là "căn bậc chính". Tại thời điểm này, chúng ta chỉ cần chú ý đến câu trả lời này.
Bước 2. Sử dụng máy tính bỏ túi
Mặc dù tốt nhất là bạn có thể làm toán bằng tay, nhưng có rất nhiều máy tính trực tuyến có sẵn để tính các căn bậc hai.
- Tìm nút căn bậc hai trên máy tính thông thường.
- Trong máy tính trực tuyến, nhập trực tiếp số bạn muốn tìm giá trị căn bậc hai và nhấp vào nút. Máy tính sẽ hiển thị cho bạn giá trị căn bậc hai.
Lời khuyên
-
Luôn ghi nhớ một vài hình vuông hoàn hảo quan trọng:
- 02 = 0, 12 = 1, 32 = 9, 42 = 16, 52 = 25, 62 = 36, 72 = 49, 82 = 64, 92 = 81, 102 = 100,
- Cũng hãy nhớ hình vuông hoàn hảo này: 112 = 121, 122 = 144, 132 169, 142 = 196, 152 = 225, 162 = 256, 172 = 289…
- Cũng lưu ý điều này: 102 = 100, 202 = 400, 302 = 900, 402 = 1600, 502 = 2500, …
