- Tác giả Jason Gerald [email protected].
- Public 2024-02-01 14:16.
- Sửa đổi lần cuối 2025-01-23 12:52.
Tất cả những gì bạn cần để tính tốc độ trung bình là tổng lượng dịch chuyển. hoặc thay đổi vị trí và tổng thời gian. Hãy nhớ rằng vận tốc cũng tính toán hướng và tốc độ của một đối tượng, vì vậy hãy bao gồm một hướng trong câu trả lời của bạn, chẳng hạn như "phía bắc", "phía trước" hoặc "bên trái". Nếu bài toán tính toán tốc độ của bạn cũng liên quan đến gia tốc không đổi, bạn có thể tìm hiểu một cách nhanh chóng để tìm ra câu trả lời thậm chí còn dễ dàng hơn.
Bươc chân
Phương pháp 1/2: Tính vận tốc trung bình của dịch chuyển và thời gian

Bước 1. Hãy nhớ rằng vận tốc bao gồm cả tốc độ và hướng của một vật
Vận tốc mô tả tốc độ thay đổi vị trí của một đối tượng. Điều này không chỉ liên quan đến tốc độ di chuyển của vật thể mà còn liên quan đến hướng của nó. "100 mét trên giây về phía nam" là một giá trị tốc độ khác với "100 mét trên giây theo hướng đông".
- Đại lượng có hướng gọi là đại lượng vectơ '. Có thể phân biệt đại lượng này với đại lượng không hướng gọi là đại lượng vô hướng bằng cách viết mũi tên phía trên biến. Ví dụ, ký hiệu v đại diện cho tỷ lệ, trong khi ký hiệu v → đại diện cho tốc độ hoặc tốc độ + hướng. Ký hiệu v được sử dụng trong bài viết này thể hiện tốc độ.
- Trong các bài toán khoa học, bạn nên sử dụng mét hoặc các đơn vị đo lường khác để thể hiện khoảng cách, trong khi đối với các mục đích hàng ngày, bạn có thể sử dụng bất kỳ đơn vị nào bạn thích.
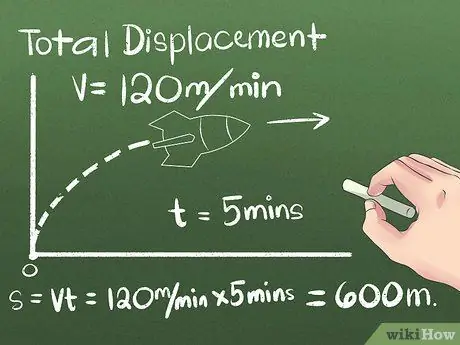
Bước 2. Tìm giá trị độ dời tổng
Độ dịch chuyển là sự thay đổi vị trí của một đối tượng hoặc khoảng cách và hướng giữa điểm bắt đầu và điểm kết thúc của nó. Có thể bỏ qua hướng di chuyển của vật thể trước khi đến vị trí cuối cùng, bởi vì chỉ tính đến khoảng cách giữa điểm đầu và điểm cuối. Đối với ví dụ đầu tiên, chúng ta sẽ sử dụng một đối tượng chuyển động với tốc độ không đổi theo một hướng:
- Giả sử một tên lửa đang chuyển động về phía bắc trong 5 phút với vận tốc không đổi là 120 mét / phút. Để tính vị trí cuối cùng, sử dụng công thức s = vt hoặc sử dụng tư duy thực tế để tính quãng đường tên lửa đi được sau đó (5 phút) (120 mét / phút) = 600 mét về phía bắc từ điểm xuất phát.
- Đối với các bài toán liên quan đến gia tốc không đổi, bạn có thể giải chúng với s = vt + at2, hoặc sử dụng phương pháp ngắn được mô tả trong phần khác để tìm câu trả lời.
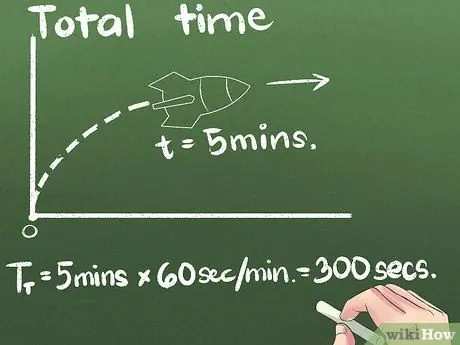
Bước 3. Tìm tổng thời gian đã sử dụng
Trong ví dụ của chúng tôi, tên lửa đang di chuyển về phía trước trong 5 phút. Bạn có thể biểu thị tốc độ trung bình trong bất kỳ đơn vị thời gian nào, nhưng thứ hai là đơn vị tiêu chuẩn khoa học quốc tế. Chúng tôi sẽ thay đổi đơn vị giây trong ví dụ này: (5 phút) x (60 giây / phút) = 300 giây.
Ngay cả trong các bài toán khoa học, nếu câu hỏi sử dụng giờ hoặc một đơn vị thời gian lớn hơn, thì việc tính tốc độ trước tiên sẽ dễ dàng hơn, sau đó chuyển câu trả lời cuối cùng thành mét / giây
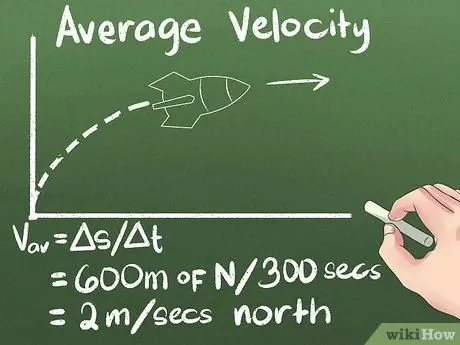
Bước 4. Tính vận tốc trung bình là độ dời theo thời gian
Nếu bạn biết một vật đang chuyển động bao xa và mất bao lâu để đến đó, bạn sẽ biết nó đang chuyển động với tốc độ như thế nào. Vì vậy, với ví dụ chúng tôi đang sử dụng, tốc độ trung bình của tên lửa là (600 mét về phía bắc) / (300 giây) = 2 mét / giây về phía bắc.
- Hãy nhớ bao gồm một hướng (chẳng hạn như "phía trước" hoặc "phía bắc").
- Trong công thức vav = s / Δt. Biểu tượng delta có nghĩa là "thay đổi", vì vậy s / Δt có nghĩa là "thay đổi vị trí trong một khoảng thời gian."
- Tốc độ trung bình có thể được viết là vav, hoặc dưới dạng v với một đường ngang phía trên nó.

Bước 5. Giải quyết các vấn đề phức tạp hơn
Nếu một đối tượng thay đổi hướng hoặc tốc độ, đừng nhầm lẫn. Tốc độ trung bình vẫn là "chỉ" được tính toán từ tổng lượng dịch chuyển và tổng thời gian. Điều gì xảy ra giữa điểm bắt đầu và điểm kết thúc, bạn có thể bỏ qua. Sau đây là một số ví dụ về một vật chuyển động với cùng độ dịch chuyển và tổng thời gian, và do đó có cùng vận tốc trung bình:
- Anna đi về phía tây với vận tốc 1 mét / s trong 2 giây, sau đó đột ngột tăng tốc lên 3 mét / giây và tiếp tục đi về phía tây trong 2 giây. Tổng độ dịch chuyển là (1 m / s về phía tây) (2 giây) + (3 m / s về phía tây) (2 giây) = 8 mét về phía tây. Tổng thời gian là 2 giây + 2 giây = 4 giây. Vậy tốc độ trung bình là 8 mét tây / 4 giây = 2 mét / giây về phía tây.
-
Bart đi về phía tây với tốc độ 5 mét / giây trong 3 giây, sau đó quay lại và đi về phía đông với tốc độ 7 mét / giây trong 1 giây. Chúng ta có thể coi chuyển động theo hướng đông là "chuyển động âm theo hướng tây" nên tổng độ dịch chuyển là = (5 mét / giây theo hướng tây) (3 giây) + (-7 m / s theo hướng tây) (1 giây) = 8 mét. Tổng thời gian = 4 giây. Tốc độ trung bình = 8 mét về phía tây / 4 giây = 2 mét / giây về phía tây.
-
Charlotte đi về phía bắc 1 mét và sau đó đi về phía tây 8 mét, sau đó đi về phía nam 1 mét. Thời gian để hoàn thành toàn bộ hành trình là 4 giây. Vẽ sơ đồ trên một mảnh giấy và bạn sẽ thấy điểm cuối cách điểm đầu 8 mét về phía tây, vì vậy giá trị này là độ dịch chuyển. Tổng thời gian mất là 4 giây, vậy tốc độ trung bình là 8 mét tây / 4 giây = 2 mét / giây về phía tây.
Phương pháp 2/2: Tính vận tốc trung bình của gia tốc cố định

Tính vận tốc trung bình Bước 6 Bước 1. Coi vận tốc ban đầu và gia tốc không đổi
Giả sử bài toán của chúng ta là "Một xe đạp đang chuyển động sang phải với vận tốc 5 m / s, gia tốc không đổi là 2 m / s2. Nếu xe đạp này chuyển động trong 5 giây thì vận tốc trung bình của nó là bao nhiêu?"
Nếu đơn vị "mét / giây2"để làm bạn bối rối, hãy viết nó là" mét / giây / giây "hoặc" mét trên giây trên giây ". Gia tốc 2 mét / giây / giây có nghĩa là tốc độ tăng 2 mét trên giây mỗi giây.

Tính vận tốc trung bình Bước 7 Bước 2. Sử dụng gia tốc để tìm vận tốc cuối cùng
Gia tốc, được ký hiệu bởi ký hiệu a, là tốc độ thay đổi của vận tốc (hoặc tốc độ). Tốc độ tăng với tốc độ tăng không đổi. Bạn có thể vẽ một bảng sử dụng gia tốc để tìm tốc độ tại các thời điểm khác nhau trong suốt hành trình của xe đạp. Chúng ta cần tạo bảng này để tìm điểm kết thúc của vấn đề (tại t = 5 giây), nhưng chúng ta sẽ tạo một bảng dài hơn để giúp bạn dễ dàng nắm bắt khái niệm này:
- Tại thời điểm xuất phát (thời điểm t = 0 giây), xe đạp đang chuyển động với vận tốc 5 mét / s.
- Sau 1 giây (t = 1), xe đạp chuyển động với vận tốc 5 mét / giây + at = 5 mét / giây + (2 mét / giây2) (1 giây) = 7 mét / giây.
- Lúc t = 2, xe đạp chuyển động sang phải với vận tốc 5+ (2) (2) = 9 mét / giây.
- Lúc t = 3, xe đạp chuyển động sang phải với vận tốc 5+ (2) (3) = 11 mét / giây.
- Lúc t = 4, xe đạp chuyển động sang phải với vận tốc 5+ (2) (4) = 13 mét / giây.
- Lúc t = 5, xe đạp chuyển động sang phải với vận tốc 5+ (2) (5) = 15 mét / giây.

Tính vận tốc trung bình Bước 8 Bước 3. Sử dụng công thức này để tìm tốc độ trung bình
Nếu và "chỉ" nếu gia tốc không đổi thì vận tốc trung bình sẽ bằng giá trị trung bình của tổng vận tốc cuối và vận tốc ban đầu. (vNS + vtôi)/2. Đối với bài toán ví dụ ở trên, vận tốc ban đầu của xe đạp là vtôi 5 mét / giây. Sau khi tính toán, vận tốc cuối cùng là vNS 15 mét / giây. Cộng hai giá trị này với nhau, chúng ta nhận được (15 mét / giây + 5 mét / giây) / 2 = (20 mét / giây) / 2 = 10 mét / giây hướng bên phải.
- Hãy nhớ bao gồm hướng, trong trường hợp này là "đúng".
- Thuật ngữ này có thể được viết là v0 (vận tốc tại thời điểm 0, hay vận tốc ban đầu) và v (vận tốc cuối cùng).

Tính vận tốc trung bình Bước 9 Bước 4. Hiểu công thức vận tốc trung bình một cách trực quan
Để tìm vận tốc trung bình, chúng ta có thể sử dụng vận tốc tại bất kỳ điểm nào và tìm trung bình cho tất cả chúng. (Đây là định nghĩa của giá trị trung bình.) Vì điều này đòi hỏi tính toán hoặc thời gian vô hạn, hãy hiểu công thức này một cách trực quan hơn. Thay vì tính từng thời điểm, hãy tính vận tốc trung bình của hai mốc thời gian và xem kết quả. Một thời điểm gần điểm bắt đầu đi xe đạp đi chậm và một điểm khác gần điểm cuối xe đạp chạy nhanh.

Tính vận tốc trung bình Bước 10 Bước 5. Kiểm tra lý thuyết trực quan
Sử dụng bảng trên để xác định vận tốc tại các thời điểm khác nhau. Một số cặp đáp ứng tiêu chí của chúng tôi là (t = 0, t = 5), (t = 1, t = 4) hoặc (t = 2, t = 3). Bạn cũng có thể kiểm tra công thức này với các giá trị t khác với số nguyên, nếu bạn muốn.
Cho dù bạn chọn cặp điểm nào thì vận tốc trung bình tại thời điểm đó sẽ luôn bằng nhau. Ví dụ: ((5 + 15) / 2), ((7 + 13) / 2) hoặc ((9 + 11) / 2) tất cả đều bằng 10 mét / giây ở bên phải

Tính vận tốc trung bình Bước 11 Bước 6. Hoàn thành phần giải thích trực quan
Nếu chúng ta sử dụng phương pháp này với danh sách mỗi lần được thực hiện, chúng ta sẽ tiếp tục tính giá trị trung bình của nửa đầu chuyến đi và nửa sau của chuyến đi. Thời gian cần cho mỗi nửa là như nhau, vì vậy không có tốc độ nào bị mất khi chúng ta đếm xong.
- Vì một trong hai cặp sẽ cho cùng một kết quả, giá trị trung bình của các tốc độ này cũng sẽ giống nhau. Trong ví dụ của chúng tôi, tốc độ của toàn bộ là "10 mét / giây về phía bên phải" sẽ vẫn là 10 mét / giây về phía bên phải.
- Chúng ta có thể tìm thấy giá trị này bằng cách tính giá trị trung bình của bất kỳ cặp nào, ví dụ vận tốc ban đầu và vận tốc cuối cùng. Trong ví dụ của chúng tôi, các tốc độ này đạt được ở t = 0 và t = 5, và có thể được tính bằng công thức trên: (5 + 15) / 2 = 10 mét / giây ở bên phải.

Tính vận tốc trung bình Bước 12 Bước 7. Hiểu công thức này về mặt toán học
Nếu bạn cảm thấy thoải mái hơn với các bằng chứng được viết ra dưới dạng công thức, bạn có thể bắt đầu với công thức để tính quãng đường đã đi với giả sử gia tốc không đổi và suy ra công thức từ đó:
- s = vtôit + lúc2. (Về mặt kỹ thuật là s và t, hoặc thay đổi vị trí và thay đổi theo thời gian, nhưng bạn cũng sẽ hiểu nếu viết s và t.)
- Tốc độ trung bình vav được định nghĩa là s / t, vì vậy hãy nhập công thức ở dạng s / t.
- vav = s / t = vtôi + tại
- Gia tốc x thời gian bằng với sự thay đổi của tổng vận tốc, hay vNS - vtôi. Vì vậy, chúng ta có thể thay thế "at" trong công thức và nhận được:
- vav = vtôi + (vNS - vtôi).
- Đơn giản hóa: vav = vtôi + vNS - vtôi = vtôi + vNS = (vNS + vtôi)/2.
Lời khuyên
- Vận tốc khác với tốc độ vì vận tốc là đại lượng vectơ trong khi tốc độ là đại lượng vô hướng. Đại lượng vectơ liên quan đến cả hướng và độ lớn, trong khi đại lượng vô hướng chỉ liên quan đến độ lớn.
- Nếu đối tượng đang chuyển động theo một chiều, chẳng hạn như trái-phải, bạn có thể sử dụng số dương để biểu thị một hướng (chẳng hạn như phải) và số âm để biểu thị hướng khác (trái). Viết ký hiệu này ở đầu trang của bạn để mọi người đọc tác phẩm của bạn rõ ràng.






