Chỉ cần bạn biết số đo của hai góc còn lại thì việc tìm góc thứ ba của một tam giác rất dễ dàng. Bạn chỉ cần trừ tổng của hai góc đi 180 độ. Tuy nhiên, cũng có những cách khác mà bạn có thể sử dụng để tìm góc thứ ba của tam giác nếu hình dạng của bài toán hơi khác một chút so với bình thường. Nếu bạn muốn biết cách tìm góc thứ ba của một tam giác, hãy làm theo hướng dẫn dưới đây.
Bươc chân
Phương pháp 1/3: Sử dụng thước đo của hai góc khác
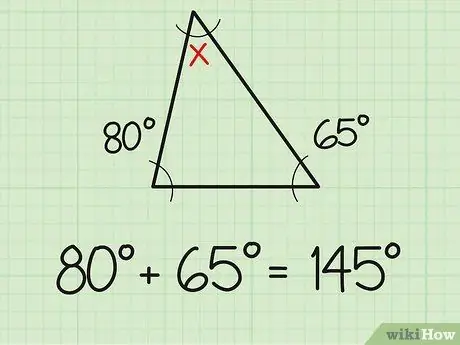
Bước 1. Cộng hai góc đã biết
Một sự thật bạn nên biết là tổng ba góc của một tam giác luôn bằng 180 độ. Vì vậy, nếu bạn đã biết số đo hai góc của một tam giác thì việc tìm góc thứ ba sẽ đơn giản như làm các bài toán cộng trừ đơn giản. Đầu tiên, cộng hai số đo góc mà bạn đã biết. Ví dụ, hai góc đã biết là 80 và 65 độ. Cộng cả hai lại với nhau (80 + 65), và bạn sẽ có được 145 độ.
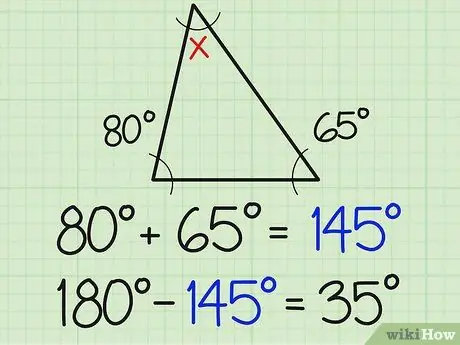
Bước 2. Chia số đó cho 180
Tổng ba góc của một tam giác luôn bằng 180 độ. Do đó, góc thứ ba phải bằng 180 khi cộng vào tổng hai số đo của góc đã biết. Trong ví dụ trên, điều này có nghĩa là 180-154 = 35.
Bước 3. Viết câu trả lời của bạn
Bây giờ bạn đã có câu trả lời cho góc thứ ba (trong ví dụ là 35 độ). Nếu bạn vẫn còn nghi ngờ, hãy xem cho chính mình. Cộng ba góc lại với nhau, bạn sẽ nhận được kết quả là 180. Nếu không, thì phép tính của bạn đã sai. Đối với ví dụ này, 80 + 65 + 35 = 180. Nếu nó là chính xác, nó có nghĩa là bạn đã giải quyết vấn đề.
Phương pháp 2/3: Sử dụng các biến
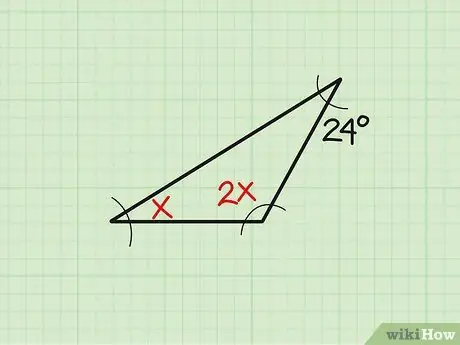
Bước 1. Viết ra vấn đề
Đôi khi, kích thước của góc hiện có được thể hiện ở dạng thay đổi. Hãy lấy ví dụ sau: “Tìm góc“x”của một tam giác nếu ba góc lần lượt là“x”,“2x”và 24.” Đầu tiên, hãy viết ra vấn đề.
Bước 2. Cộng tất cả các số đo góc
Nguyên tắc bạn phải nhớ vẫn được giữ nguyên. Vì vậy, trước tiên hãy cộng ba góc trong bài toán, đó là "x + 2x + 24 = 3x + 24".
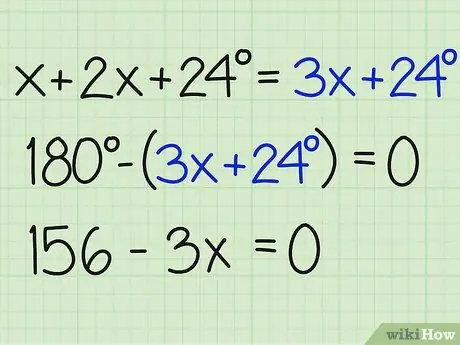
Bước 3. Chia tổng các góc cho 180
Bây giờ, hãy chênh số đó đi 180 độ để tìm x và tìm ra câu trả lời cho bài toán. Đảm bảo rằng bạn kết thúc phương trình bằng không. Đây là cách nó được viết:
- 180- (3x + 24) = 0
- 180-3x-24 = 0
- 156-3x = 0
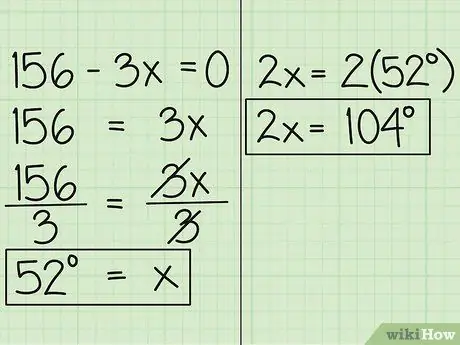
Bước 4. Tìm giá trị của x
Bây giờ, di chuyển biến sang phía bên kia của phương trình, và bạn sẽ nhận được 156 = 3x. Sau đó, chia phương trình cho 3, bạn nhận được x = 52. Điều này có nghĩa là số đo của góc được biểu thị theo x là 52 độ. Góc còn lại, được biểu thị bằng 2x là 52 độ nhân với 2, là 104 độ.
Bước 5. Kiểm tra kết quả của bạn
Nếu bạn muốn chắc chắn rằng câu trả lời của mình là chính xác, chỉ cần cộng ba số đo góc mà bạn đã tìm ra câu trả lời. Nếu kết quả là 180, có nghĩa là câu trả lời của bạn là đúng. Đối với ví dụ này, 52 + 104 + 24 = 180.
Phương pháp 3/3: Sử dụng các phương pháp khác
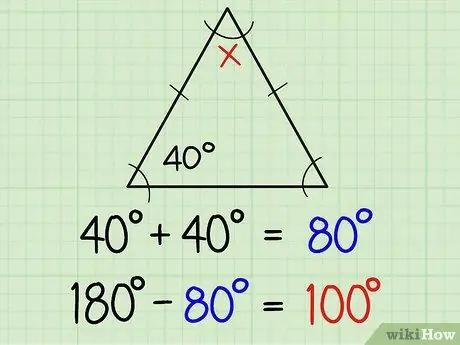
Bước 1. Tìm các góc của tam giác cân
Một tam giác cân có hai cạnh bên bằng nhau và hai góc bằng nhau. Hai cạnh bằng nhau thường được đánh dấu bằng một vạch nhỏ ở giữa đường cạnh, nghĩa là hai góc đối diện trên đường thẳng có cùng số đo. Nếu bạn đã biết kích thước của một góc, bạn sẽ tự động biết góc còn lại. Đây là lời giải thích thêm:
Nếu một trong các góc bằng nhau là 40 độ thì góc còn lại là 40 độ. Bằng cách đó, bạn có thể tìm thấy tất cả ba góc có hiệu giữa tổng của 40 + 40 (tức là 80) và 180, hay nói cách khác là 180-80 = 100
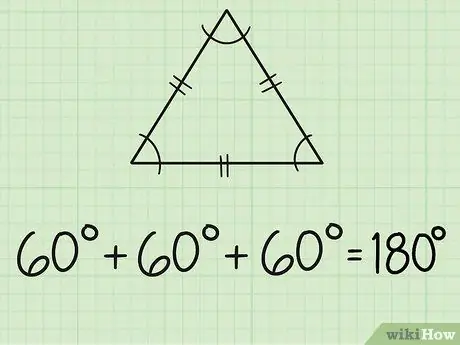
Bước 2. Tìm các góc của một tam giác đều
Một tam giác đều có ba cạnh bằng nhau và ba góc bằng nhau. Mỗi bên thường được đánh dấu bằng hai đường ngắn ở giữa. Vì cả ba góc đều bằng nhau nên có nghĩa là tất cả các góc đều đo được 60 độ, vì 180/3 = 60.
Bước 3. Tìm góc thứ ba trong tam giác vuông
Giả sử bạn có một tam giác vuông, với một trong các góc nhọn là 30 độ. Vì tam giác là một góc vuông, có nghĩa là một trong các góc, cụ thể là góc vuông, phải đo 90 độ. Sau đó sử dụng nguyên lý tam giác, hiệu số giữa tổng hai góc (90 + 30 = 120) bằng 180, thì bạn sẽ có 180-120 = 60 độ.
