- Tác giả Jason Gerald [email protected].
- Public 2023-12-16 11:46.
- Sửa đổi lần cuối 2025-01-23 12:52.
Nếu bạn đã hiểu, việc chuyển đổi phân số thông thường sang số thập phân không khó. Để chuyển đổi các phân số thông thường sang số thập phân, bạn có thể sử dụng phép chia dài, phép nhân hoặc thậm chí là máy tính nếu bạn không muốn tính toán bằng tay. Khi bạn đã thành thạo phương pháp, bạn sẽ có thể dễ dàng chuyển đổi phân số thành số thập phân.
Bươc chân
Phương pháp 1/4: Với phép chia dài
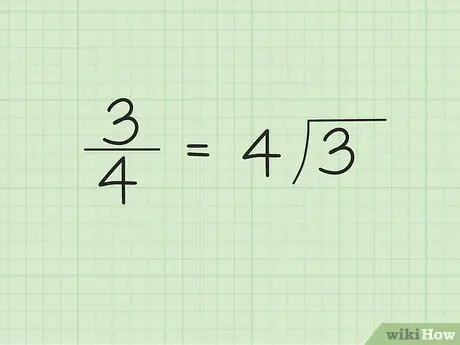
Bước 1. Viết mẫu số bên ngoài / bên trái của ký hiệu số chia và tử số bên trong / bên phải của ký hiệu số chia
Ví dụ: giả sử chúng ta muốn chuyển 3/4 thành số thập phân. Viết “4” bên ngoài / bên trái của ký hiệu số chia và “3” bên trong / bên phải của ký hiệu số chia. “4” là số bị chia và “3” là số bị chia.

Bước 2. Viết “0”, sau đó là dấu thập phân (dấu phẩy), phía trên ký hiệu số chia
Vì nó là một phân số đếm, kết quả phải nhỏ hơn một, vì vậy bước này rất quan trọng. Sau đó, viết dấu thập phân, sau đó là “0”, sau số “3” ở / bên phải của ký hiệu số chia. Mặc dù “3” bằng “3, 0”, số 0 cho phép “3, 0” chia cho “4”.

Bước 3. Tính toán câu trả lời bằng cách sử dụng phép chia dài
Với phép chia dài, hiện tại, dấu thập phân có thể bị bỏ qua nên bạn chỉ cần tính 30 chia cho 4. Dưới đây là cách thực hiện:
- Đầu tiên, chia 3, 0, được tính là 30, cho 4. Từ 4 đến 30 gần nhất là 4 x 7 = 28, còn lại 2. Vì vậy, hãy viết “7” sau “0” phía trên số chia và “28” dưới “3, 0”trong / bên phải của ký hiệu số chia. Dưới 28, viết "2", phần dư của 30 trừ đi 28.
- Tiếp theo, viết “0” sau “3, 0” để nó trở thành “3, 00”, có thể được coi là “300”, bên trong / bên phải của ký hiệu số chia. Vì vậy, số 0 có thể được hạ xuống bên phải của "2" để "20" chia hết cho "4".
- “20” chia cho “4” bằng “5”. Vì vậy, hãy viết "5" sau "0,7" phía trên ký hiệu số chia để nó trở thành "0,75".

Bước 4. Viết câu trả lời cuối cùng
Vì vậy, "3" chia cho "4" bằng "0,75". Viết ra câu trả lời. Hoàn thành.
Phương pháp 2/4: Phân số tạo ra số thập phân lặp lại
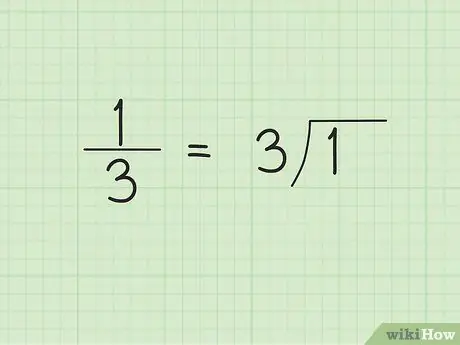
Bước 1. Thực hiện phép chia dài
Khi bạn bắt đầu phép chia các chữ số dài, bạn có thể không dự đoán được rằng kết quả sẽ là một số thập phân lặp lại. Ví dụ: giả sử chúng ta muốn chuyển phân số chung 1/3 thành dạng thập phân. Viết 3, hoặc mẫu số, ở bên ngoài / bên trái của ký hiệu số chia và 1 bên trong / bên phải của ký hiệu số chia.

Bước 2. Viết số 0, sau đó là dấu thập phân, phía trên ký hiệu số chia
Vì kết quả phải nhỏ hơn 1, bước này chuẩn bị câu trả lời được viết dưới dạng thập phân. Dấu thập phân cũng phải được viết ở bên phải của số “1” nằm ở / bên phải của ký hiệu số chia.
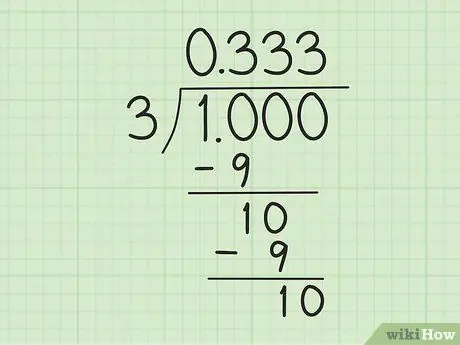
Bước 3. Bắt đầu tính toán chia dài
Bắt đầu bằng cách biến “1” thành “1, 0”, được tính là “10”, sao cho nó chia hết cho “3”. Tiếp theo, thực hiện các bước sau:
- Chia 10 cho 3. Dùng 3 x 3 = 9 để tạo số dư là 1. Vì vậy, viết 3 vào bên phải chữ “0” phía trên ký hiệu số chia và trừ 10 cho 9 để được số dư là 1.
- Viết số "0" vào bên phải số "1" (phần dư của 10 trừ đi 9 ở bước trước) dưới đây để được số "10" khác. Khi chia “10” cho “3” một lần nữa, quy trình tương tự được lặp lại: viết “3” vào bên phải chữ “3” đầu tiên phía trên ký hiệu số chia và trừ “10” mới cho “9”.
- Tiếp tục cho đến khi một mẫu được hình thành. Bạn biết điều gì đó kỳ lạ? Sự phân chia này có thể kéo dài mãi mãi. 10 luôn chia hết cho 3: sẽ luôn có "1" ở dưới cùng và "3" mới sau số thập phân phía trên ký hiệu số chia.
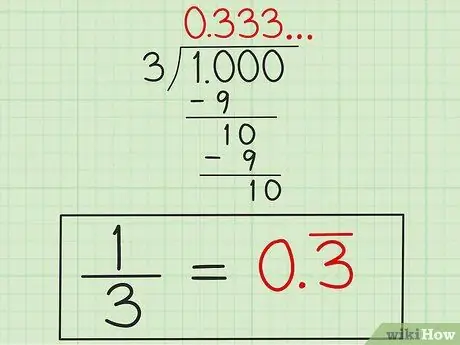
Bước 4. Viết câu trả lời
Sau khi biết rằng "3" sẽ tự lặp lại, hãy viết câu trả lời là "0, 3" với một dòng phía trên số "3" (hoặc "0, 33" với một dòng phía trên cả hai số "3") như một dấu hiệu cho thấy số "3" nó tiếp tục lặp lại. Câu trả lời này ở dạng thập phân 1/3 vì 1 chia cho 3 sẽ không kết thúc bằng chính nó.
Có nhiều phân số tạo ra số thập phân lặp lại, chẳng hạn như 2/9 (“0, 2” với “2” lặp lại), 5/6 (“0, 83” với “3” lặp lại) hoặc 7/9 (“0, 7”với“7”tiếp tục lặp lại). Dạng này luôn xảy ra khi mẫu số là bội của 3 và tử số không thể chia hết cho mẫu số
Phương pháp 3/4: Bằng phép nhân

Bước 1. Tìm số có thể nhân với mẫu số của phân số để tạo ra 10, 100, 1.000 hoặc bất kỳ số nào là cơ số 10
Đây có thể là một cách dễ dàng để chuyển phân số thành số thập phân mà không cần sử dụng phép chia dài hoặc máy tính. Đầu tiên, chỉ cần tìm một số có thể nhân với mẫu số của phân số để được 10, 100, 1.000, v.v. Để thực hiện việc này, trước tiên hãy chia 10, rồi 100, rồi 1.000, v.v. cho mẫu số cho đến khi bạn nhận được một số nguyên. Thí dụ:
- 3/5. 10/5 = 2,2 là một số nguyên. 2 có thể được nhân với 5 để tạo ra 10. Vì vậy, 2 có thể được sử dụng.
- 3/4. 10/4 = 2, 5. 2, 5 không phải là số nguyên. 100/4 = 25. 25 là số nguyên. 25 có thể nhân với 4 để tạo thành 100. Vì vậy, 25 có thể được sử dụng.
- 16/5. 10/16 = 0, 625, 100/16 = 6, 25, 1,000/16 = 62, 5, 10,000 / 16 = 625. 625 là số nguyên đầu tiên thu được. 625 có thể được nhân với 16 để có 10.000. Vì vậy, 625 có thể được sử dụng.
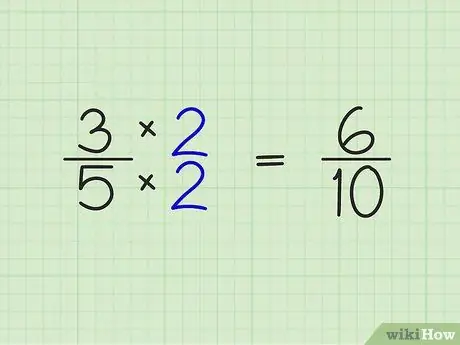
Bước 2. Nhân tử số và mẫu số của phân số với số nguyên có được ở bước trước
Bước này khá dễ dàng. Chỉ cần nhân các số trên và dưới phân số với số nguyên mà bạn đã nhận được ở bước trước. Thí dụ:
- 3/5 x 2/2 = 6/10
- 3/4 x 25/25 = 75/100
- 5/16 x 625/625 = 3.125 / 10000

Bước 3. Viết câu trả lời cuối cùng
Câu trả lời là tử số được đánh dấu bằng một số thập phân theo số 0 ở mẫu số. Chỉ cần đếm xem có bao nhiêu số 0 ở mẫu số. Nếu chỉ có 1 0 ở mẫu số, hãy di chuyển dấu thập phân sang bên trái 1 chữ số, v.v. Thí dụ:
- 3/5 = 6/10 = 0, 6
- 3/4 = 75/100 = 0, 75
- 5/16 = 3.125/10.000 = 0, 3125
Phương pháp 4/4: Với Máy tính

Bước 1. Chia tử số cho mẫu số
Phương pháp này rất dễ dàng. Chỉ cần sử dụng máy tính để chia tử số, số ở đầu phân số, cho mẫu số, số ở cuối phân số. Ví dụ: giả sử bạn muốn chuyển 3/4 thành số thập phân. Chỉ cần nhấn “3”, sau đó là ký hiệu chia ("÷ '"), sau đó "4" và cuối cùng là ký hiệu bằng ("=").

Bước 2. Viết ra câu trả lời bạn nhận được
Đáp số là 0,75. Vậy dạng thập phân của phân số 3/4 chung là 0,75.
Lời khuyên
- Để kiểm tra xem câu trả lời của bạn có đúng không, hãy nhân câu trả lời với mẫu số của phân số. Nếu câu trả lời của bạn là đúng, tích của phép nhân là tử số của phân số.
- Một số phân số có thể được chuyển đổi thành số thập phân bằng cách tạo ra các phân số có thể so sánh có mẫu số là cơ số 10 (10, 100, 1.000, v.v.). Tiếp theo, sử dụng các giá trị vị trí để viết ra dạng thập phân chính xác.






