Chia phân số cho các số nguyên không khó như ta tưởng. Để chia một phân số cho một số nguyên, tất cả những gì bạn phải làm là chuyển số nguyên thành phân số, tìm nghịch đảo của phân số và nhân kết quả với phân số đầu tiên. Nếu bạn muốn biết cách thực hiện, chỉ cần làm theo các bước sau:
Bươc chân
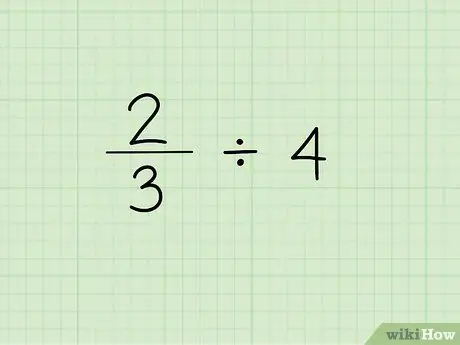
Bước 1. Viết ra vấn đề
Bước đầu tiên để chia một phân số cho một số nguyên là viết phân số theo sau là dấu chia và số nguyên bạn cần chia phân số. Giả sử chúng ta đang giải quyết vấn đề sau: 2/3 4.
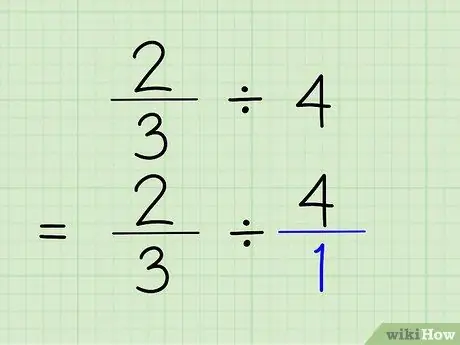
Bước 2. Chuyển số nguyên thành phân số
Để chuyển một số nguyên thành phân số, tất cả những gì bạn phải làm là đặt số nguyên phía trên số 1. Số nguyên trở thành tử số và 1 trở thành mẫu số của phân số. Nói 4/1 thực sự giống như nói 4, bởi vì bạn chỉ cho thấy rằng số chứa "1" 4 lần. Vấn đề sẽ là 2/3 4/1.
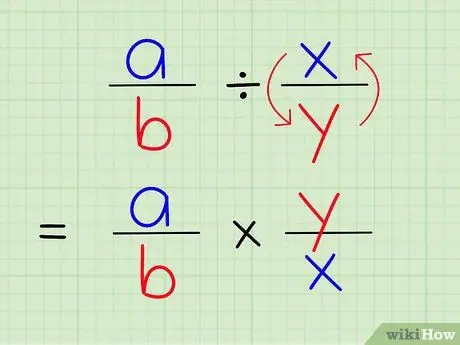
Bước 3. Chia một phân số cho một phân số khác cũng giống như nhân phân số đó với nghịch đảo của một phân số khác
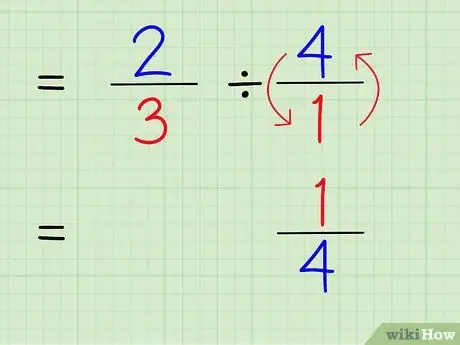
Bước 4. Viết nghịch đảo của số nguyên
Để tìm nghịch đảo của một số, hãy hoán đổi tử số và mẫu số của số đó. Do đó, để tìm số nghịch đảo của 4/1, chỉ cần hoán đổi tử số và mẫu số để số đó trở thành 1/4.
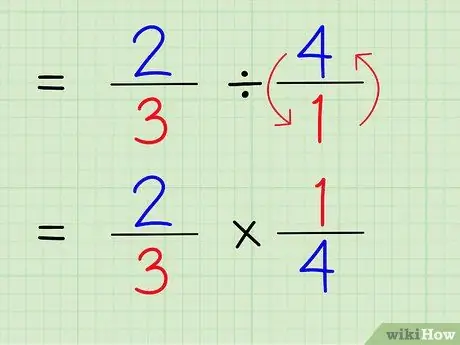
Bước 5. Đổi dấu chia thành dấu nhân
Bài toán sẽ là 2/3 x 1/4.
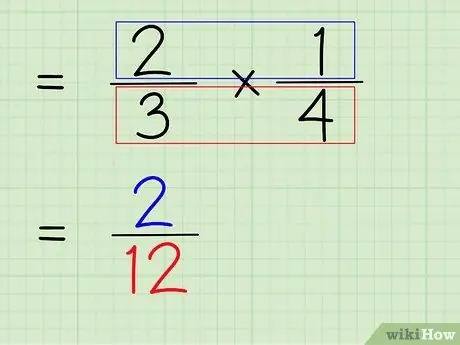
Bước 6. Nhân tử số và mẫu số của phân số
Vì vậy, bước tiếp theo là nhân tử số và mẫu số của phân số để có được một tử số và mẫu số mới làm câu trả lời cuối cùng.
- Để nhân các tử số, chỉ cần nhân 2 x 1 với 2.
- Để nhân các mẫu số, chỉ cần nhân 3 x 4 để được 12.
- 2/3 x 1/4 = 2/12
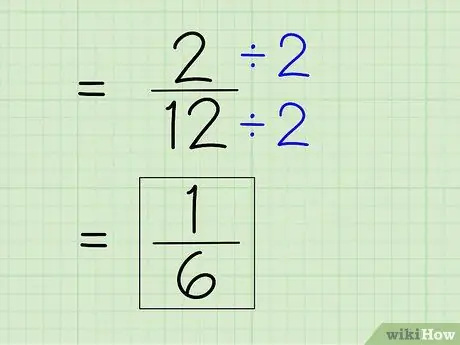
Bước 7. Đơn giản hóa phân số
Để đơn giản hóa một phân số, bạn phải tìm mẫu số nhỏ nhất, có nghĩa là bạn phải chia tử số và mẫu số cho bất kỳ số nào chia cả hai số. Vì 2 là tử số, bạn sẽ phải xem liệu 2 có thể chia hết cho 12 hay không - điều đó có thể xảy ra vì 12 là số chẵn. Sau đó, chia tử số và mẫu số cho 2 để được tử số và mẫu số mới để có một câu trả lời đơn giản.
- 2 ÷ 2 = 1
- 12 ÷ 2 = 6
- Phân số 2/12 có thể được đơn giản hóa thành 1/6. Đây là câu trả lời cuối cùng của bạn.
Lời khuyên
- Điều này là để hỗ trợ trí nhớ, một cách dễ dàng để nhớ cách thực hiện tất cả các phép tính này. Hãy ghi nhớ điều này: "Thật dễ dàng để chia phân số, đảo ngược số thứ hai và nhân!"
- Một biến thể khác của phương pháp trên là JGB / JBG. Đừng thay đổi số đầu tiên. Chuyển sang phép nhân. Đảo ngược số cuối cùng. Hoặc B trước rồi G.
- Nếu bạn hủy phép tính trước khi nhân nó, bạn có thể không cần tìm dạng đơn giản nhất của phân số vì kết quả đã ở dạng phân số đơn giản nhất mà bạn có thể thấy. Trong ví dụ của chúng ta, trước khi chúng ta nhân 2/3 × 1/4, chúng ta có thể thấy rằng tử số thứ nhất (2) và mẫu số thứ hai (4) có cùng cấp số nhân là 2, chúng ta có thể hủy bỏ trước khi tiếp tục tính toán. Điều này chuyển đổi bài toán thành 1/3 × 1/2, cho kết quả 1/6 ngay lập tức và giúp chúng tôi tiết kiệm thời gian đơn giản hóa phân số ở giai đoạn sau.
- Nếu một trong các phân số của bạn là số âm, phương pháp này vẫn khả thi; đảm bảo rằng bạn theo dõi các dấu hiệu khi bạn thực hiện các bước này.
